PROBLEM LINK:
Author: Alexey Zayakin
Testers: Hasan Jaddouh
Editorialist: Alexey Zayakin
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Math, bitwise operations, fractals
PROBLEM:
XOR-grid is define as an infinitely large grid G filled with numbers based on the following three rules:
- G[1, c] = 1 for all c \ge 1
- G[r, 1] = r for all r \ge 1
- G[r, c] = G[r - 1, c] \oplus G[r, c - 1] for all r > 1 and c > 1, where \oplus means xor
Answer T queries of the form "What is the XOR-sum of all the numbers within subgrid G[r1 \dots r2][c1 \dots c2]?".
QUICK EXPLANATION:
We can solve the problem separately for each bit. For a fixed bit the XOR-grid is just a shifted Sierpinski triangle and we just want to compute the parity of count of ones within the given rectangle. The latest can be further reduced to four instances of “Compute the parity of count of ones on some prefix-rectangle of the Sierpinski triangle”. Sierpinski triangle is a fractal and as all we need is the parity, we can ignore the parts that are repeated twice.
EXPLANATION:
First of all, we will solve the problem separately for each bit. For a fixed bit k, the three rules that define the XOR-grid transform into:
- G[1, c] = 1, if k = 0 and G[1, c] = 0 otherwise, for all c \ge 1
- \displaystyle G[r, 1] = \left \lfloor \frac{r}{2^k} \right \rfloor \mod 2, for all r \ge 1
- G[r, c] = G[r - 1, c] \oplus G[r, c - 1], for all r > 1 and c > 1
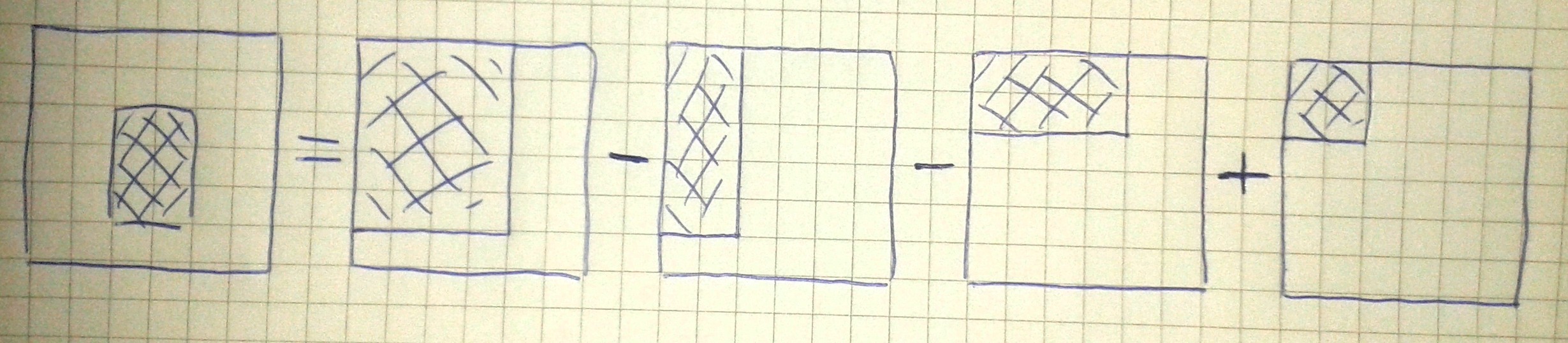
This grid looks extremely similar to Sierpinski triangle, just with a different base conditions (i.e. the first row and column). But looking a bit closer, one can notice that the XOR-grid (of a fixed size) is just a part of the Sierpinski triangle, XOR-grid for k = 0 is just a Sierpinski triangle without the first row, XOR-grids of size 4 \times 14 for k = 2 and 5 \times 8 for k = 1 are shown on the picture below:

In general, one can prove, that a subrectangle of Sierpinski triangle starting at (2^{62} - 2^k + 1, 2^k) is the same as 10^{18} \times 10^{18} XOR-grid for bit k.
Thus our problem reduces to finding the XOR-sum of some subrectangle of the Sierpinski triangle. We will use the standard idea to reduce the problem of “calculate some sum on an arbitrary rectangle” to “calculate the same sum on four prefix-rectangles” and inclusion-exclusion to get the sum on an arbitrary rectangle.
To calculate the XOR-sum on a prefix-rectangle we will use the fact that Sierpinski triangle is a fractal, so it has a lot of repeating parts and due to the x \oplus x = 0 property of the xor operation, the parts that repeat exactly twice contribute 0 to the total XOR-sum.

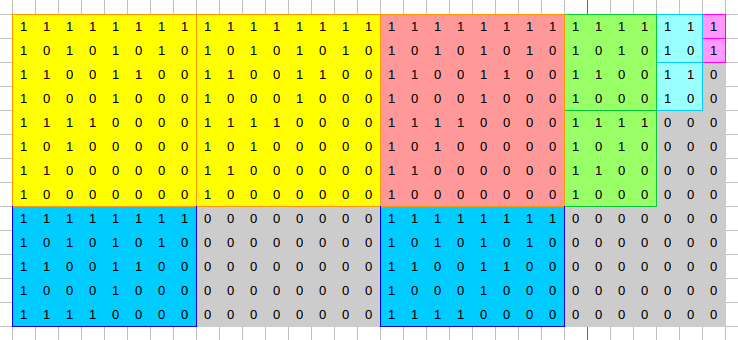
Observing the pictures above we can create a solution: we find the maximal power of two (denote it with k) that is \le min(w, h), where w and h are the width and height of the prefix-rectangle. The prefix-rectangle contains some number of full fractal parts of size 2^k \times 2^k.
In case this number is even (the first picture above), we can see that the only unpaired part of the prefix-rectangle is the bottom-right red part. It is easy to see that the red part is the same as a prefix-rectangle of an appropriate size, thus we can just continue recursively with a smaller prefix-rectangle (the smallest side became at least two times smaller, thus the total runtime would be \mathcal{O}(\log w)).
In case the number of full fractal parts of size 2^k \times 2^k is odd (the second picture above), the only unpaired part is one of the full fractal parts. It is easy to prove by induction that every full fractal contains an odd number of ones (or precisely 3^p), thus our prefix-rectangle has XOR-sum equal to 1.
Right now we have a working solution that would receive an AC verdict, but it is still possible to further improve it a bit. Let’s try to understand what are the cases when the number of full fractals is odd. For simplicity assume 2^k \le w \le h, then we have \displaystyle \left \lfloor \frac{h}{2^k} \right \rfloor full fractals and this number is odd if the k-th bit of h is 1. We already know that the k-th bit of w is 1 as well. Based on the above observation one can prove that the XOR-sum of a prefix-rectangle (w, h) is 1 if and only if the bitwise AND of w and h is not zero.
Time Complexity:
\mathcal{O}(\log n) per test case, where n = max(r2, c2).