Xdcomp - editorial

general
, , , , ,
1

PROBLEM LINK:

Practice
Contest: Division 1
Contest: Division 2

Setter: Daanish
Tester: Alexey Zayakin and Yash Chandnani
Editorialist: Taranpreet Singh

DIFFICULTY:

Medium

PREREQUISITES:

Tree DP, Combinatorics and Observation.

PROBLEM:

Given a tree with N nodes, each node marked with a value A[i] and a value x, Find out the number of ways to remove a subset of edges such that each of the new tree formed has xor-sum of all values in tree equal to x. Print this number of ways modulo 10^9+7.

Let us call a subtree with xor-sum x as special.

QUICK EXPLANATION

  • If the xor-sum of all nodes is not x or 0, it is not possible to achieve xor sum x by removing any subset of edges. The number of ways being zero in this case.
  • Now, If a node has subtree xor-sum x, it shall be divided into an odd number of special trees, removing an even number of edges. Alternatively, if xor-sum of the subtree of a node is zero, it shall be divided into even number of special trees, by removing an odd number of edges.
  • For each node, we can calculate the number of ways to remove odd as well as even number of edges such that each of the generated trees is special. For now, ignore the fact that subtree xor of current node may differ from 0 or x.
  • Number of ways to remove the number of edges from the subtree of a node is an XOR-convolution of the number of ways to remove edges from the subtree of each of its children.
  • If subtree xor of a node (not being the root) is x, the number of ways to remove an odd number of edges become the sum of the number of ways to remove odd and even number of edges. Similarly, if the subtree xor-sum is 0, the number of ways to remove even number of edges become the sum of the number of ways to remove odd and even number of edges.
  • Corner case x = 0. Here, the number of ways is 2^x where x is the number of nodes with subtree xor being zero excluding root, only if subtree xor of the whole tree is zero. Otherwise, there is no way to split given tree into special subtrees.

EXPLANATION

First of all, Let’s handle the base case, where x = 0. Here, Suppose we an edge connecting a subtree with xor-sum zero to its parent. The subtree xor is not affected at all. Hence, for every node (except root) which have subtree xor-sum zero, can be removed independently. If there are x such nodes, considering each combination, there are a total of 2^x ways to remove edges.

Coming to general case, we can notice that x \oplus y \oplus y = x. This means, that if from the subtree of a node, we disconnect even number of special subtrees, the xor-sum of the tree is not affected. But if an odd number of special subtrees is disconnected, the xor-sum of remaining nodes in the subtree is XORed by x.

Let’s denote DPE_u denote the number of ways to remove even number of edges from subtree of node u and edge connecting u and its parent (except for root), while DPO_u denote the number of ways to remove odd number of edges from subtree of node u plus the edge connecting node u and its parent. It’s clear that initially, DPE_x = 1 (We have the DP state a bit unusual, but it eases implementation. It’s possible to solve it normal way too).

Suppose a node x has two direct children, say u and v. It can be easily seen, that DPE_x = DPE_u*DPE_v + DPO_u*DPO_v while DPO_x = DPE_u*DPO_v+DPO_u*DPE_v. Can you spot the pattern? It’s basically the xor convolution. We can also visualize it as the polynomial multiplication, where each node is represented by a variable of degree 1, x^i being the number of ways to remove i edges.

Now comes the trouble. We have the option of removing the edge connected current node with its parent (assuming current node is not root). If we do not remove that edge, the number of ways is just the XOR convolution of the number of ways to remove edges for children of the current node.

Suppose we have subtree xor of current node as x. In this case, if we were removing even number of edges, we always have the choice to remove an odd number of edges by removing the edge connecting current node with its parent, thus removing an odd number of nodes for each way we can remove an even number of nodes. Thus, we increase DPO_x by DPE_x if the subtree xor of a node is x and the node is not root.

Similarly, if the subtree xor of a node is 0, and we have removed an odd number of edges, we have the choice to remove the edge connecting the current node to its parent resulting in removing an even number of edges. Hence, if subtree xor of the node is zero, we can remove an even number of edges for every way we were able to remove odd number of edges. Hence, we can simply increase DPE_x by DPO_x if the subtree xor of the node is 0 and the node is not root.

Consider example tree where node 2, 3 and 6 are labeled 1, and rest are labeled zero. x = 1 for this example.

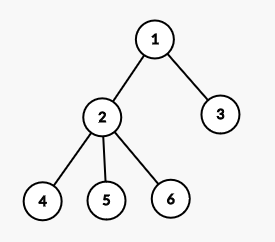
alt text

For node 6, DPE_6 = 1 as we may not remove edge 2-6. DPO_6 = 1 if we choose to remove edge 2-6.

For node 5, DPE_5 = 1 as we may not remove edge 2-5. DPO_5 = 0 as we cannot remove any odd number of edges, making special subtrees.

For node 4, DPE_4 = 1 as we may not remove edge 2-4. DPO_4 = 0 as we cannot remove any odd number of edges, making special subtrees.

For node 3, DPE_6 = 1 as we may not remove edge 1-3. DPO_6 = 1 if we choose to remove edge 1-3.

For node 2, we have to perform XOR convolution of number of ways of all its children, where DPE is coefficient of x^0 and DPO is coefficient of x^1. Clearly, we have (1+1*x^1)*(1+0*x^1)*(1+0*x^1) which equates to (1+x^1). This means, before considering edge 1-2, DPE_2 = 1 and DPO_2 = 1. Subtree xor of node 2 is 0, so, for every way to remove odd number of edges (excluding the edge connecting node and its parent), we can remove even number of edges if we choose to remove edge connecting node and its parent. So, we have DPE_2 = DPE_2+DPO_2 = 2 and DPO_2 = 1.

For node 1, we once again need to perform the same convolution. We have the product as (1+1*x^1)*(2+1*x^1) = (2+3*x^1+1*x^2) Important thing here to notice is that coefficient of x^2 represent number of ways to remove 2 edges. We only care about parity here, so polynomial (3+3*x^1) represent the same number of ways. Since this node is root, we cannot have any edge connecting this node to its parent.

Finally, xor-sum of the tree is 1, so, we can split this tree by removing an even number of edges, the answer to our problem is DPE_0, while if xor-sum is zero, the answer is DPO_1.

Those facing problem with this “convolution thing” refer the box below.

Click to view

You can simply think of this it as, parity of numbers after addition. Two odds make an even, two evens make an even, while one odd and other even makes an odd. I intentionally included this “convolution thing”. :stuck_out_tongue:

Time Complexity

Time complexity is O(N).

AUTHOR’S AND TESTER’S SOLUTIONS:

Setter’s solution
Tester’s solution
Editorialist’s solution

Feel free to Share your approach, If it differs. Suggestions are always welcomed. :slight_smile:

4 Likes
2

I intentionally included this "convolution thing".
I’m upvoting due to this "convolution thing". This was the first intuition which came to my mind. I used it. + Some stress tests to get AC. :stuck_out_tongue:

3

I used similar approach, but can’t fully map it to the editorial description.

I ended up deriving a formula for merging results from children’s nodes subtrees to a parent node. Not sure if those formulas just describe xor convolution approach.

Here is the approach:

  1. Merge the original tree into a tree of nodes x and 0. Basically, starting from leaves, XOR a child node into a parent node if the child node is not x or zero. If x=0 then the answer is trivial power of two. Otherwise:

  2. For each node of the merged tree (all references to a tree below mean merged tree) let’s maintain two numbers {m,n}:

  • n: number of ways to split the subtree of that node such that the node is in the connected group that XORs to x
  • m: number of ways to split the subtree that the node is in the connected group that XORs to zero.

  1. Each leaf node that is equal to x gets {m,n} = {0,1} and each leaf node equal to zero gets {m,n} = {1,0}.

  2. For each node in a merged tree we can calculate {m,n} bases on the values for children nodes subtrees:

  • Let’s calculate two numbers: A = Product of m[i] and B = Product of (2*n[i]+m[i]), where product is taken over all children nodes i.
  • If the node is equal to x, then {m,n} = 1/2 * {B-A, B+A}
  • If the node is equal to 0, then {m,n} = 1/2 * {B+A, B-A}
  1. The final answer is n of the root.

https://www.codechef.com/viewsolution/22935893

4 Likes
4
  1. For node 6, DPE6=1 as we may not remove edge 2-6. DPO6=1 if we choose to remove edge 5-6.

There is no edge between 5-6.

  1. Finally, xor-sum of the tree is 1, so, we can split this tree by removing an even number of edges, the answer to our problem is DPE0, while if xor-sum is zero, the answer is DPO1.

What is DPE0 here?

Am i the only one who can’t understand editorial of this problem even after reading many times and checking so many solutions. I don’t understand how to use this convolution thing.

1 Like
5

Basically for the convolution thing ,(a0*x0+a1*x1)*(b0x0+b1*x1)*(..)*(..)..... = (a0*b0*x0+(a0*b1+a1*b0)*x1)*(...)*(...)... and that makes sense as to make even edges ,(even+odd)*(even+odd)*...
and finally take for even which is coefficient of x0…

1 Like
6

Point 1 was a typo, corrected. :slight_smile:

Which part u didn’t understand?

7

Is there a tradition of codechef to never provide the link properly at first and fix it later.

PS :- Sorry for being humouristic. Please fix the link.

3 Likes
8

I don’t get the convolution thing , can someone please explain that ?

I am also gonna add my solution here since I think its much simpler :

During the DFS , whenever the subtree xor becomes equal to X or 0 , remove the edge from that node to its parent. Shrink all the forests obtained to a node each and give it a value of 1 if xor was equal to X otherwise 0.Connect the removed edges again, the problem is reduced to finding the no. of partitions of the decomposed tree such that each each forest has an odd sum. This can be done using DP on children.
dp[i][0] = no. of ways to get even sum till the i^{th} child.

dp[i][0] = dp[i-1][0]*(odd(c_i)+even(c_i)) + dp[i-1][1]*odd(c_i) (the odd case can be derived by swapping 1 for 0) where odd and even store the number of partitions such that the all parts that have been removed are odd and current is odd/even.

2 Likes
9

best solution i’ve found based on the editorial
https://www.codechef.com/viewsolution/22866349

10

Can anyone explain how we arrived at this result :- “DPEx=DPEu∗DPEv+DPOu∗DPOv and DPOx=DPEu∗DPOv+DPOu∗DPEv.”