PROBLEM LINK:
Author: Vitaliy Herasymiv
Tester: Istvan Nagy
Editorialist: Amit Pandey
DIFFICULTY:
Easy.
PREREQUISITES:
Simulation.
PROBLEM:
Given a robot and N\times N grid, find any valid sequence of moves starting from (1,1) such that there are no more than three consecutive turns that moved the robot in the same direction and robot covers each cell at-least once.
QUICK EXPLANATION:
Start at (1,1) and at each step, consider two consecutive rows and visit in pattern DRURDRU(D=Down, R=Right, U=Up). Once both rows are done, jump to another pair of rows. Take care of hurdles using some specific technique. See explanation for details.
EXPLANATION:
There might be many possible solutions to the problem, lets discuss one of them. We need to derive an strategy which will be covering all of the cells using minimum number of steps and later we have to increase the steps to stop ourselves to go to forbidden cells.
Start at co-ordinate (1,1), Consider two rows at a time. visit in the pattern DRURDRU.
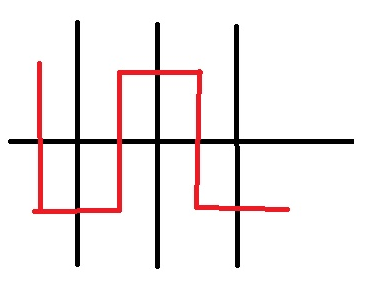
If in any row, we found a forbidden cell then it will fall in one of these two cases.
- We are visiting in pattern DRURDRU. Suppose while we are going up after going right and get to a cell which is forbidden, then we may continue in right direction and then go up(the pattern DRUR becomes DRRU..). See the first one in the image.
- We get a forbidden cell while we are going into right and previous one was the up. In this case, we may go down again, go right twice and then go up(DRURDR becomes DRUDRUR..).
In second case, we are visiting a cell more than once but we are skipping a cell as well. So, number of steps will not exceed number of cells. So, if N is even then in worst case we are using O(N^2) number of steps. If N is odd, we are using (N-1)^{th} row twice so, we using N(N+1) number of step in worst case.
While connecting the row pair ending we will be using at most 5 steps while there is some forbidden cell, which can be shown using the following image. If there is no forbidden cell, we can do it in lesser number of steps.
Maximum number of step would be \le N(N+1) + 5(\frac{N}{2}) = N(N+\frac{7}{2})
It is easy to see we are never taking three steps in same direction in any of the case. In first two cases, we are taking at most two steps in the same direction. While we are switching the pair of rows, we are taking three steps in one direction in the same direction and later changing the direction just after third step.
Solution:
Setter’s solution can be found here
Tester’s solution can be found here
Changed the difficulty to medium. The problem is definitely more difficult than the STRAB.