TWOROADS - Editorial

[utkarsh_lath]

Problem Link:

Practice

Contest

Difficulty:

Hard

Pre-requisites:

High School Geometry

Problem:

Given a set S of N points in plane, you have to draw two lines such that sum of squares of distance of each point from nearest line is smallest.

Explanation:

The first thing one realizes about this problem is that the business of taking minimum of the distances is causing all the trouble. If we had to draw a single line to optimize sum of squares of its distance from all points, it would be a piece of cake. High school calculus can be used to find the optimum equation of the line. Here is a brief sketch:

Let the equation of optimum line be y +mx +c = 0. The square of distance of a point (x0,y0) from this line is (y0 + mx0 + c)²/(1 + m²). Therefore, sum of squares of distance of all points is

(Y2 + m²X2 + c² * N + 2 * m * XY + 2 * Y * c + 2 * m * X * c) / (1 + m²)
where Y2 = sum_i y_i², X2 = sum_i x_i², XY = sum_i y_ix_i, X = sum_i x_i, Y = sum_i y_i, N = sum_i 1

We need to find optimum m and c. To do this, first differentiate with respect to c to get c as a (linear)function of m, plug it in the above, and differentiate with respect to m to get optimum value. Refer to solutions at the end for more precise details. Assuming that the one line case can be solved in constant time, given X, Y, XY, N, X2, Y2, we can now proceed.

Now imagine the optimal pair of lines. Let the lines be named A and B. Every point in our set S is closer to exactly one of A and B. Let S_A be the set of points in our S closer to A than B. Similarly define S_B. Note that S_B = S - S_A.

Now suppose, by some magic, we managed to find the set S_A. Then we would again be done. This is because line A is the optimal line for the set S_A, and line B is the optimal line for remaining points.

Cool ! So, we now have a O(N * 2^N) solution, which basically iterates over all subsets S_A of S, and reports the solution.

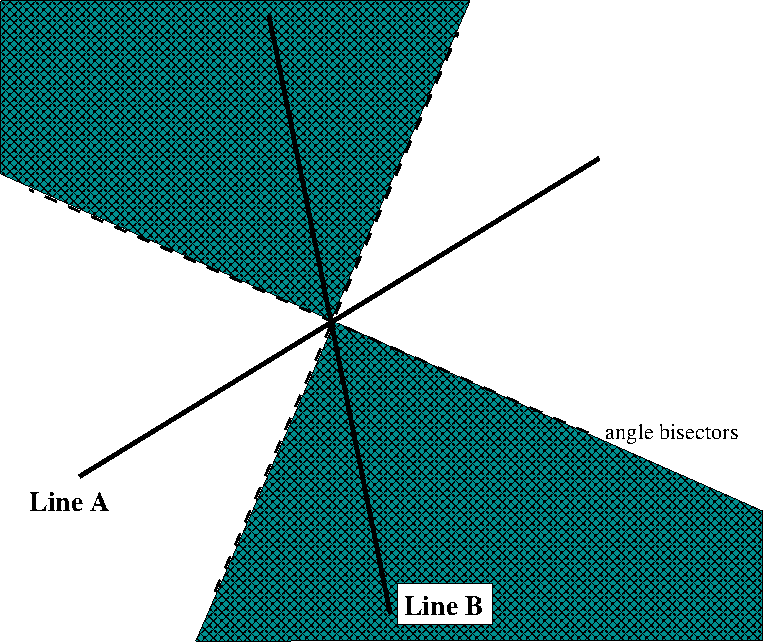
Obviously, the next step is to note that sets S_A and S_B cannot be arbitrary. If we are given a pair of lines A and B, then S_A consists of exactly those points in S which do not lie in the colored region. Similarly, S_B consists of those points which lie in the colored region. Justification is very straightforward and left to the reader. The colored region can be identified by a pair of perpendicular lines. For any two perpendicular lines L, M, let R_L,M denote the the first and third quadrant of the co-ordinate system defined by line L, M. Formally, R_L,M = {points P | tan ∠ PXL ≥ 0}, X being intersection point of L and M.

Due to discussion above, we know that the set S_A cannot be arbitrary. The set S_A has to be such that there exist two perpendicular lines L and M, so that S_A = S ∩ R_L,M.

In fact, we give a list Z of pairs of lines(i.e. Z={(L₁, M₁), (L₂,M₂), … (L_M,M_M)}) such that, for any arbitrary pair of lines (L, M) we can obtain another pair of lines (L’, M’) which satisfies the following

• S ∩ R_L,M = S ∩ R_L’,M’
• (L’, M’) ∈ Z

In other words, the possible lines L and M can be infinite in number, but we can find a finite set of pairs of lines which still induce all possible partitions of the given set S. In fact we can show that the required number of pairs of lines is polynomial in N.

Here is how to obtain L’, M’ from any L, M.

• Translate L, parallel to itself towards right, until L hits some point P₁ ∈ S. Stop translating when it is infinitesimally small distance away from P₁.
  

• Now translate M, parallel to itself towards right, until it hits some point P₂ ∈ S. Again stop translating when distance between line and point becomes infinitesimally small.
  

• Rotate both L and M clockwise so that i) M remains perpendicular to L, ii) One end point of L is fixed at P₁, iii) One end point of M is fixed at P₂. The intersection point of L and M moves in a circle with P₁P₂ as diameter. Stop rotating when one of L or M hits some point P₃ ∈ S. Again, stop rotating when it is infinitesimally small distance away from P₃.
  

  

Now it is clear that the new lines L’, M’ obtained by above process still induce same partition of S as L, M did. Moreover, L’, M’ are completely defined by

• Points P₁, P₂, P₃.
• One bit indicating whether P₃ was hit from above or below. It doesn’t matter whether L’ actually hit P₃ or M’ because they are interchangeable.

The set Z of all possible final pairs (L’, M’) obtained after translation/rotation has size 2n³, and can be easily enumerated. We can solve the problem in O(n^3) overall time as well, because the partitions imposed by these lines can be interconverted by adding/removing single points, and hence (X, Y, XY, X2, Y2) tuple can be re-calculated in constant time. See the solutions below for exact details.

Setter’s Solution:

Can be found here

Tester’s Solution:

Can be found here

Editorialist’s Solution:

Can be found here

[forthright]

When I first read the problem, I realized I had to find regression line of N points. In this case instead of one, I had to find two. I didn’t know how to find one line, let alone two. So I googled and found an interesting paper on K-line mean : http://people.csail.mit.edu/dannyf/mscthesis.pdf

In the paper, they describe an O(n^3) algorithms for 2-line mean. They use vectors and linear algebra to solve the problem (I think!). If only I was good at linear algebra then maybe I could have understood this article (all those matrix decomposition and vector products boggled my mind). I tried studying linear algebra books for few days but they didn’t cover these advanced topics (SVD for example). Plus reading 500+ pages of a books didn’t seem efficient.

So anybody here solved the problem using this paper or linear algebra? Any resource that will help me with linear algebra (and this problem).

[betlista]

Hi guys, can someone help me to find the roads for those three inputs?

6
-1 10
1 10
-3 12
3 12
-1 -10
1 -10

and

5
-1000 1000
0 999
1000 1000
-1 -1000
1 -1000

and

9
-1 -1000
1 -1000
-500 1000
500 1000
0 997
1000 999
1000 998
-1000 999
-1000 998

Testers solution fails for all the inputs. Setter’s and editorialist’s solution returns 0.414866845 for first input, 0.133333333 for second and 0.666666667 for the third, but it seems to me less than I’d expect. If possible, give me the roads in y = a*x + b form, thanks.

[betlista]

I noticed, that both setter’s and editorialist’s solution prints printf("%.9lf\n", ans/N); is that average instead of “minimum sadness” ?

[baukaman]

If someone can fail this solution:
Consider all lines that is pairwise combination of given points. For each line we will consider it’s top and bottom parts. For each part we solve our known calculus thing. I got WA. Someone plz tell what test fails this approach ?

[betlista]

for my inputs, your solution returns

0.66666666666666662966
0.13333333333333333148
0.82539682539682535101

Can you describe your approach more precisely? As I understood, you split the points by line. In which part are point on that line?

[baukaman]

Yep , u r correct. I did all possible cases. Both to bottom(1 case). Both to top(1 case). one top one bottom(2 cases). So overall 4 cases for each pair of points.

[baukaman]

How you googled it ? I couldn’t found any good topics

[baukaman]

look page 23, solution to our problem ))

[utkarsh_lath]

first:
0.535184 * x + 1 * y + -10.1315 = 0
-7.28871 * x + 1 * y + 9.95538 = 0

second:
0 * x + 1 * y + -999.667 = 0
0 * x + 1 * y + 1000 = 0

third:
0 * x + 1 * y + -999 = 0
1 * x + 0 * y + -0 = 0

[utkarsh_lath]

I have given best solution for @betlista 's inputs. Now you can check where you went wrong

[betlista]

@utkarsh_lath thanks a lot

[betlista]

I’d like to ask for tips, how to solve such hard problem, respectively how to test them. First option is to create some test cases with known results. But even for those I asked here earlier, my expected result was wrong. Only idea I found is to find mean line for every triple of points, calculate distances so I will have some upper bound. I can do that for 50 points. Typically I implement some brute force solution to get answers for random test cases, but here I have no idea how to achieve this…

[n2n]

Another paper which solves a similar problem in O(N^3) can be found at http://infoscience.epfl.ch/record/164483/files/nscan3.PDF

[betlista]

@kevinsogo you are correct, negative coordinates are not valid input, but once you have working algorithm, it’s not so important, but that’s why tester’s solution “fails”…

[utkarsh_lath]

You could at least get a O(2^n) solution as described above. That is not too hard once you give a bit of thought to the problem.

The difficult part was to get it down to O(n^3). Probably the central idea was to realize the angle bisector thing. The rest of ideas used in our solutions is fairly common. When you need to bring down an infinite number of possibilities to a small finite number in geometrical setting, this method (method described in editorial) is the way to go.

[betlista]

The idea of splitting point between sets S_A and S_B is not difficult, but I got confused because when I choose points for S_A and use mean line for those, maybe some point from S_B are closer to that line, but now it seems to me, that this is no problem at all…

[baukaman]

Thanks a lot. I found bug in my calculus formula. Plus dividing by only one line will not work. It is evident for me now. It is great relief to find out where I was wrong.

[baukaman]

I think approach to this problem is N^3logN.

Two outer loops gives us n^2. And inside it we have sorting(respect to projections to line) which is NlogN. Am I correct ?

[betlista]

Good spot @utkarsh_lath is that sorting necessary ?