Problem Link:
Author: Pavel Sheftelevich
Tester: Kanstantsin Sokal
Editorialist: Sunny Aggarwal
Difficulty:
Easy
Pre-Requisites:
Implementation, Observation, Game Theory, Dynamic Programming.
Problem Statement
Consider a 2 player game where a coin is placed at (1, 1) on a NxM board. In a turn, a player can move the coin either right or up with the constraints that a player can’t move coin more than 2 cells right and more than 3 cells up. We are asked to find the winner of the game given N, M and the player who will move first.
Brief Explanation
Given problem can be modelled as standard Nim Game problem and can be solved using sprague-grundy-theorem. According to the theorem, given configuration will be a loosing configuration for the player who is to make move if grundy number corresponding to the configuration is 0.
Solution
It should be noted that a player is only allowed to move a coin either to the right or to up with the given constraints. It means a player will either move the coin row wise or column wise in his turn as shown in the figure given below.
We assign grundy number to every subgame according to which size of the pile in the Game of Nim it is equivalent to. When we know how to play Nim we will be able to play this game as well.
int grundyNumber(position pos) {
moves[] = possible positions to which I can move from pos
set s;
for (all x in moves) insert into s grundyNumber(x);
//return the smallest non-negative integer not in the set s;
int ret=0;
while (s.contains(ret)) ret++;
return ret;
}
The following table shows grundy numbers for an 8 x 8 board:
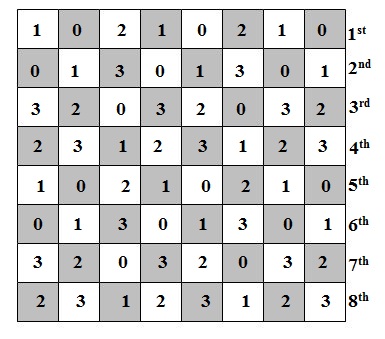
We have constructed this table starting from the top right cell. You can find code for this table generation here.
Why is the pile of Nim equivalent to the subgame if its size is equal to the grundy number of that subgame?
-
If we decrease the size of the pile in Nim from A to B, we can move also in the subgame to the position with the grundy number B. (Our current position had grundy number A so it means we could move to positions with all smaller grundy numbers, otherwise the grundy number of our position would not be A.)
-
If we are in the subgame at a position with a grundy number higher than 0, by moving in it and decreasing its grundy number we can also decrease the size of pile in the Nim.
-
If we are in the subgame at the position with grundy number 0, by moving from that we will get to a position with a grundy number higher than 0. Because of that, from such a position it is possible to move back to 0. By doing that we can nullify every move from the position from grundy number 0.
According to sprague grundy theorem, a state will be a loosing state if its grundy number = 0. You can learn more about impartial games and similiar problems here.
Using above theorem, we can simply answer whether a given configuration of board is a winning configuration or a loosing configuration by finding its corresponding grundy number but wait in our problem N, M can be as large as 10^6 and number of possible states can be as large as 10^{12}. How to find grundy number for a given state efficiently then ?
Notice from the grundy table given above that the 1^{st} row is same as 5^{th} row, 2^{nd} row is same as 6^{th} row, 3^{rd} row is same as 7^{th} row and 4^{th} row is same as 8^{th} row. More generally, we can say two rows x & y will be same if x % 4 == y % 4. Does this observation help us ? Yes, now number of states has been reduced to 4 * 10^6. We can precompute a table where N can take values from [1, 4] and M can take values from [1, 10^6] as follows:
C++ Code:
int state[5][1000001];
int IsWinning(int i, int j) {
if( i == 1 && j == 1 )
return 0;
int &ret = state[i][j];
if( ret != -1 ) return ret;
ret = 0;
for(int k=1; k<=2; k++)
if(j - k > 0)
ret |= (1 - IsWinning(i, j-k));
for(int k=1; k<=3; k++)
if(i-k > 0)
ret |= (1 - IsWinning(i-k, j));
return ret;
}
int main() {
memset(state, -1, sizeof state);
for(int i=1; i<=4; i++) {
for(int j=1; j<=1000000; j++) {
state[i][j] = solve(i, j);
}
}
int t; cin >> t;
while( t-- ) {
int n, m;
cin >> n >> m;
puts(state[(n-1)%4+1][m] ? "Tuzik" : "Vanya");
}
return 0;
}
This solution will get AC if implemented properly and efficiently.
Can we further improve our solution ?
Yes, there is one more observation to consider that every column repeats itself after 3 column. So, we just need to compute all the states where N \in [1, 4] and M \in [1, 3] i.e only 12 states and then to check whether a state with N, M is winning or not, we just need to check state with N'=(N-1)\%4+1, M'=(M-1)\%3+1.
C++ Code:
int state[5][8];
int IsWinning(int i, int j) {
if( i == 1 && j == 1 )
return 0;
int &ret = state[i][j];
if( ret != -1 ) return ret;
ret = 0;
for(int k=1; k<=2; k++)
if(j - k > 0)
ret |= (1 - IsWinning(i, j-k));
for(int k=1; k<=3; k++)
if(i-k > 0)
ret |= (1 - IsWinning(i-k, j));
return ret;
}
int main() {
memset(state, -1, sizeof state);
for(int i=1; i<=4; i++) {
for(int j=1; j<=3; j++) {
state[i][j] = solve(i, j);
}
}
int t; cin >> t;
while( t-- ) {
int n, m;
cin >> n >> m;
puts(state[(n-1)%4+1][(m-1)%3+1] ? "Tuzik" : "Vanya");
}
return 0;
}
Alternatively, grundy numbers ( also known as NimSum ) for a given state N, M can be computed directly using formulla ((N-1)\%4) xor ((M-1)\%3).
Time Complexity:
Variable: O(1), O(\max(M)), O(\max(N))
Space Complexity:
Variable: O(1), O(\max(M)), O(\max(N))
Similiar Problems:
Solution:
Setter’s solution can be found here
Tester’s solution can be found here
Feel free to post comments if anything is not clear to you.