TRIQUERY - Editorial

editorial
, , , ,
1

Problem Link:

Practice

Contest

Difficulty:

Medium

Pre-requisites:

line-sweep, rank-query DS

Problem:

Given N points (Xi, Yi), and Q queries (x, y, d), find for each query how many of the N points lie within or on the boundary of the triangle formed by the triangle A(x+d, y), B(x,y), C(x,y+d).

Explanation:

This problem is solved by offline processing of the queries and using a line-sweep. Unlike most line-sweep problems, where you would sweep a (vertical) line across the X-axis (or a horizontal line across the Y-axis), and keep an active set etc, in this problem, you sweep a line of the form “x+y=c” across the plane. (Note that the slope of the hypotenuse of our query-triangle is parallel to such a sweep-line and hence the motivation for such a choice).

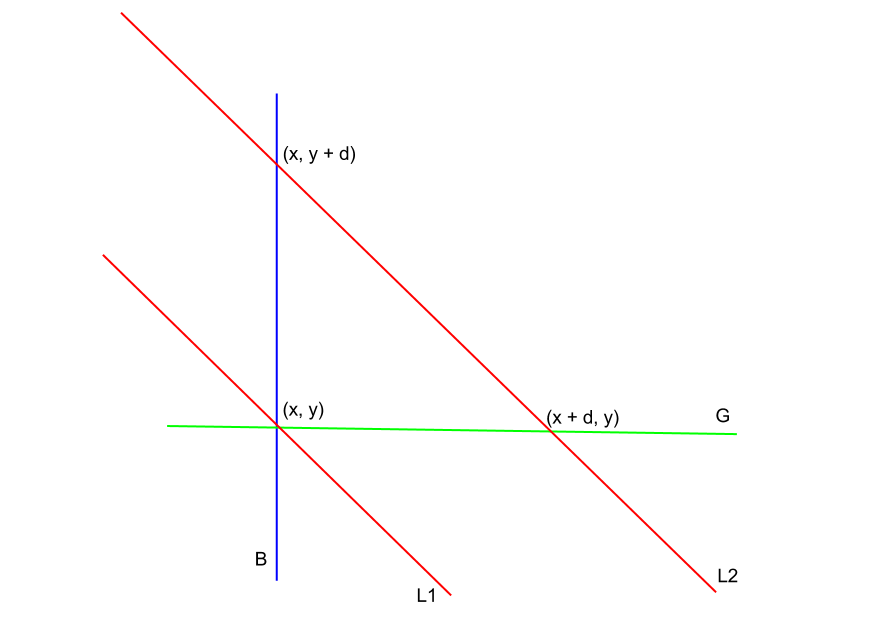
Query Triangle
In the figure shown, we want to find the number of points in or within the boundary of L2, B and G. If we are processing lattice points in the plane in order of sweep-line, and have so far seen points below L2, we just need to remove from this set of seen points, the ones that are below G or to the left of B.

This suggests that we have an active set of “seen points”, wherein at time T, their X+Y <= T (i.e. T defines our sweep-line). From this set of seen points, we want to remove those whose X <= x, or whose Y <= y. If we store the seen points in 2 Binary Indexed Trees (BIT): one for their X coordinate, one for their Y coordinate, and query for how many points <= x, or <= y, then using principle of inclusion-exclusion, we get that the required answer = Total seen points - num(points left of B) - num(points below G) + num(points left of B and below G).

How do we find num(points left of B and below G)?

The answer lies in the line L1. When our sweep-line was at L1, we have: Total number of points seen so far = points either left of B or below G. Again by Inclusion-Exclusion, we have Total points seen so far = num(points left of B) + num(points below G) - num(points left of B and below G). From this, we can calculate num(points left of B and below G).

Thus, our algorithm is as follows:

For each of the N lattice points (X, Y), associate an event “Add (X,Y) to active set at time point X+Y”.

For every query (x, y, d), associate 2 events. Event 1 is: “Find num(points having X<=x and Y<=y) at time point x+y”.

Event 2 is: “Answer required query at time point x+y+d”.

Lets call the first kind of event as “Add point” event, the second kind of event as “L1-type” event, and the third kind as “L2-type” event.

Finally, care has to be taken to ensure that we include the boundary of our triangle formed by B, G, L2. This is done by breaking ties of time-point in the manner of L1-type event comes before any Add-point event which comes before any L2-type event.

Setter’s Solution:

Can be found here

Tester’s Solution:

Can be found here

9 Likes
2

I tried to solve this in online mode:

i stored count of points on different lines parallel to x+y=0

on query of (x,y,d) we can find points to the left of B and below G (as used in editorial) by using two segment trees.

each segment tree is built with (level,x) and (level,y) correspondence (level is line no. with respect to x+y=0)

i couldn’t get rid of RTE in my submission but is this method good enough for this problem…??

1 Like
3

Could somebody please tell me what do we mean by offline processing of points?
And also why was I getting a runtime error in my code
http://www.codechef.com/viewsolution/1802839

4

Why TLE? http://www.codechef.com/viewsolution/1808836

5

Your solution has complexity O(N * Q). Obviously it will get TLE.
Did you ever try to run your solution with N=3e5 and Q=2e5?

6

Can’t this problem also be solved by doing an orthogonal range search in 3 dimensions (between (x, y, x+y) and (x+d, y+d, x+y+d)) using range trees or kd trees?

Something like this http://www.codechef.com/viewsolution/1809831 (kd-tree, TLE, Complexity is q*(n^2/3))

Range trees with fractional cascading could solve this in O(q*((log(n))^2))

3 Likes
7

@code_master01 I tried same logic too I am getting RTE too :(…

8

How to run it with N=3e5 and Q=2e5?

9

I meant how to manually create such a test file.

10

Setter nice and clear solution!

11

Is there any other simple to implement data structure for rank-query other than balanced BST if the range of value is 10^9 ?

2 Likes
12

This is the code for manually creating a test file

#include<iostream>
#include<cstdio>
int main()
{printf("300000 200000\n");
for(int i=1;i<=500;i++)
{for(int j=1;j<=600;j++)
 printf("%d %d\n",i,j);}
for(int i=1;i<=200000;i++)
printf("%d %d %d\n",i,i,i);
return 0; }
13

then direct the output of this program to the input of ur program.
where input.txt is text file generated from the above code.
./a.out <input.txt

14

Hey Jas, not like this. I know the direct(./a.out < input.txt) thing, but I want huge random tests. Not in a serial order like this.

15

I do not get this part in the setter’s solution, please help:

int comp_pt(pt A,pt B) // For sorting points by their diagonal
{
	return A.x+A.y<B.x+B.y;
}

sort(pts,pts+n, comp_pt);

Explain this part and I will try to understand the remaining things.

16

sort(pts, pts+n, comp_pt), means sort the array “pts” from pts[0] to pts[n], using comp_pt() as the compare function.

Since the sweep line is of the form x+y=d, all the points lying to the left of the sweep line have x+y < d and all points to the right have x+y > d. So having all the points sorted w.r.t “x+y”, gives a quick way to eliminate points.

1 Like
17

thank you.

18

One generally maps your range of 10^9 values to O(10^5) actual values. (Use a STL map or set or something). The mapping should only preserve ordering of elements.

For example, if your input (into your BST) was 5, 10, 10^7, then first make the mapping


5 -> 1
10 -> 2
10^7 -> 3

and use just these mapped values in your BIT.

1 Like
19

I thought of this . but suppose we want to do online processing of queries .

20

offline mode means that you “don’t” calculate your answer of every input query separately but either you do some preprocesing before taking input or you take all the input and find answer to the all queries at the same time. [here same time means like you are going though the input queries and finding “half” answer to some queries and then coming back again and again]

1 Like