PROBLEM LINK:
Author: Shubham Singhal
Tester: Shivam Wadhwa
Editorialist: Shubham Singhal
DIFFICULTY:
MEDIUM
PREREQUISITES:
DFS, DP on Trees
PROBLEM:
Given a tree, you need to find the maximum possible sum of scores of any number of nodes, with one condition i.e nodes should be connected.
EXPLANATION:
The nice observation here is that, we can obtain any secondary tree by deleting some specific edges from our original tree.
You can see with the help of images, what we mean by secondary tree:
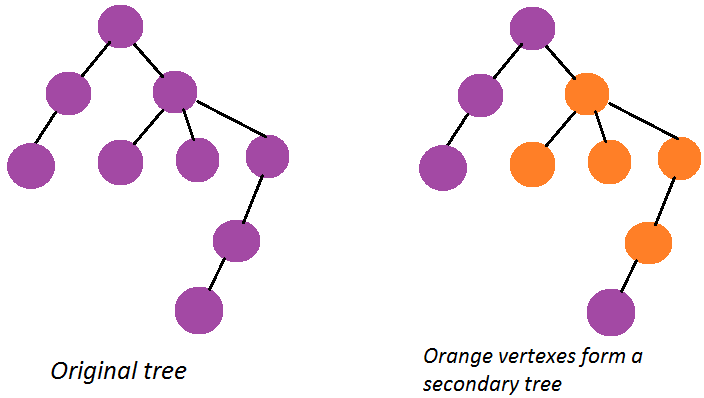
There can be many such secondary trees inside a tree. It can be either a vertex alone or maybe whole original tree too.
So our remaining task is to find such a secondary tree whose sum of scores is maximum.
This task can be easily done with the help of a DFS and DP on trees.
Let’s denote DP[i] = Maximum score which we can get by forming best secondary tree rooted at vertex i.
So, to maximize sum of secondary tree rooted at vertex i, we will add those best secondary trees which are rooted at any of the vertex i's children. So formally, we can calculate DP[i] as follows:
DP[i] = score[i];
for( every child j of vertex i)
{
if( DP[j] is greater than 0 )
DP[i] += DP[j];
}
We can calculate all DP values easily by using a DFS.
To compute our best possible score, we just need to find the maximum value among all DP[x] where 1 \le x \le N.
See author’s solution for more detail.
TIME COMPLEXITY
O(N)
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.