SUMPOWER - Editorial

editorial
, , , , , ,
1

Problem Link

Practice

Contest

Author: Ivan Safonov

Tester: Hasan Jaddouh

Editorialist: Bhuvnesh Jain

Difficulty

EASY

Prerequisites

Prefix sums, Sliding Window

Problem

You are given a string S of length N and an integer K. Consider all the (N - K + 1) substrings of S of length K. Find the sum of the hamming distance between 2 consecutive substrings, where hamming distance is defined as the number of positions where the characters of two strings differ.

Explanation

For simplicity, the editorial assumes 0-based indexing of the string.

Subtask 1: T ≤ 100, N ≤ 50

For the first subtask, a naive brute force is enough to solve it. Below is a pseudo-code for it.


	def hamming(string a, string b):
		diff = 0
		for i in [0, len(a) - 1]:
			if a[i] != b[i]:
				diff += 1
		return diff

	def solve(string s, int k):
		ans = 0
		for i in [0, k - 1]:
			sub_1 = s.substring(i, i + k - 1)
			sub_2 = s.substring(i + 1, i + k)
			ans += hamming(sub_1, sub_2)
		return ans

The complexity of the above approach will be O(N^2) per test case. This is not efficient for the second subtask.

Subtask 2: T ≤ 100, N ≤ 100000

For this consider, let us consider an example string S = "aabbcc" and K = 3, same as in the problem statement. Below table shows the calculation for the above naive approach.

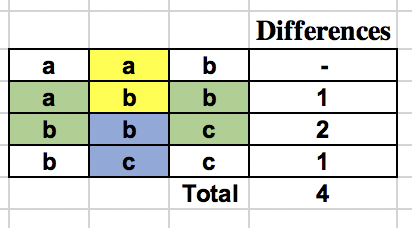
The naive approach tries to find the hamming distance of every row with the previous one and add it up. Let us see what happens when we try to find the differences along the column and them sum them up. The below table shows the calculation.

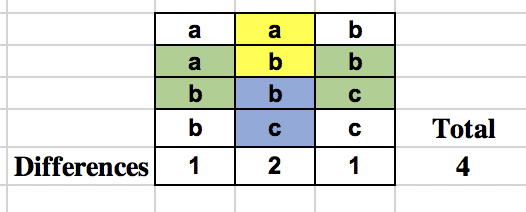
What advantage do we have while doing the above calculation in column manner? First, we don’t have to deal with full substrings. Instead, we deal with each column independently and all we care about is whether 2 consecutive characters in S are same or different.

The second one is that there is a lot of repetition in the calculation across columns, meaning that same set of different characters are repeated across many columns. For example, in the above case the pair (a, b) corresponding to letters at indices (1, 2) appears in column 1 and column 2.

So, let us store the difference array, diff, where diff[i] will be 1 if S[i] != S[i-1] else 0. using this, we can clearly see that answer for a column is just a sum of range for diff range. Using prefix sums, we can calculate the answer for every column in O(1). Then, we can add the contribution to all possible columns and find the overall answer.

Below is pseudo-code for the above approach:


	def solve(string s, int k):
		for i in [1, len(s) - 1]:
			if s[i] != s[i-1]:
				diff[i] = 1
			else:
				diff[i] = 0
		# Build prefix sum
		for i in [1, len(s) - 1]:
			diff[i] += diff[i-1]

		ans = 0
		for i in [0, k - 1]:
			ans += diff[i + (n - k)] - diff[i]
		return ans

The time complexity of the above approach will be O(N + K). The pre-computation will consist of 2 parts. First, finding the diff array and then calculating the prefix sum of diff array. Each step takes O(N) complexity. Then, we find the contribution for every column, which is K in total. The space complexity will be O(N) for this approach.

You can improve the space complexity to O(1) as well using sliding-window to approach to calculate the prefix-sums on the fly and hence the answer for every column.

For more details, you can refer to the editorialist’s solution for help.

Bonus Problem

Construct a test case where the answer will overflow i.e. will not fit inside integer type and we would require the use of “long long” in C++ and “long” in Java.

Feel free to share your approach, if it was somewhat different.

Time Complexity

O(N + K) per test case.

Space Complexity

O(N)

Solution Links

Setter’s solution

Tester’s solution

Editorialist solution

2

What is this kind of approach? (


[1])
I didn't understand this one.


  [1]: https://www.codechef.com/viewsolution/19022775
3

@mohitchandrak: Imagine a character s_i in the string that is in cell c (in the board) on the k-th step. Then the successor of that character s_{i+1} will be on the cell c in the k+1-th step, if it happens (call this an event). If s_i \ne s_{i+1}, then it requires one unit of power. Now the total power that is used over all operations can be thought of as a net effect of all such pairs (s_i, s_{i+1}), s_i \ne s_{i+1}. For each such pair, we can figure out on how many cells this event happens (it is K, except when the characters are among the first K or last K positions of the string, which is what the linked code considers).

1 Like
4

my approach is kind of common sense approach.

first step–>>> As first we calculate maximum no. of transaction an element can do that is min( n-k , k).

max no of transaction an element can do

min of:-

1: k bcoz if we have a b c d e f then c can go 3 times transaction with d then d after that c will be gone .
a b c -> b c d-> c d e-> d e f.

2: n-k bcoz if we have four element for ex a b c d , k=3 then a b c-> b c d; everyone has gone 1 transaction.

second step–>> then we calculate array of transaction element will do.

1: first element can do 1 transaction ; second can do either 2 or 1 if max limit is 1; third
element can do 3 transaction if max limit is not reached otherwise it will do transaction of max limit ;like this we build the array but

2: last element can do 1 transaction ; second last can do 2 only if max limit is not reached ; third last can do 3 if max limit is not reached else it will do that much transaction.

now ex to understand above approach

here k =3 ; just for understanding

elements; transaction array; max transaction can do;

a b c d;;;;;;;;;;;[1 1 1];;;;;;;;;;; 1

a b c d e;;;;;;;;;;;[1 2 2 1];;;;;;;;;;; 2

a b c d e f;;;;;;;;;;;[1 2 3 2 1];;;;;;;;;;;3

a b c d e f g;;;;;;;;;;;[1 2 3 3 2 1];;;;;;;;;;;3

if 8 elements then ;;;;;;[1 2 3 3 3 2 1];;;;;;;;;;;3

“similarly it go with any of k”

**third step->>>**now if s[i]!=s[i+1] then we just add the cost(count+=a[i]) as we know how many times it will go transaction with that element ; if s[i]==s[i+1] then no cost taken.

link for my code https://www.codechef.com/viewsolution/19032639

for better understanding please refere to link as code contain comments

9 Likes
5

basic approach is just to cal no of transaction bw i and i+1 that is through transaction array i created and ping me if anyone had problem

2 Likes
6

Input Test Case for overflow:
1
100000 50000
abcdefghijklmnopqrstuvwxyzabcde…(till 100000 characters)

Output
2500000000

Which will overflow and not fit in integer datatype

1 Like
7

How do we check the answer will overflow? I really don’t know why the answer exceed int. Thank you

8

The answer will exceed int as the count will be more than the maximum no. that can be stored in the int datatype. This will lead to generation of random nos.

9

Can anybody help me with this approach?


[1]


  [1]: https://www.codechef.com/viewsolution/19030972
10

Can somebody point out why I’m Getting Wrong Answer


(https://www.codechef.com/viewsolution/19025299).
11

I cannot understand the solution, how prefix sum is used to get the answer, can someone please elaborate the intuition behind the author’s solution?

12

Thanks for telling about the O(1) space complexity approach :slight_smile: It had never occurred to me.

13

Thanks for this, never heard about prefix-sum before :stuck_out_tongue:, however, I tried solving this question using segment tree, although it ended up giving TLE error on subcase #2,
my approach was to build an array ‘ARR’ of size N-1, and each index i of this array is either 1 or 0

ARR[i] = 1 denotes that string’s i-th and i+1 th character are different
and so ARR[0] denotes that i th and i+1 th character are same
so if

string is : a a b b c c

then

ARR is : 0 1 0 1 0

then using this array, build a sum-query based segment tree
ended up being *O((N-K)log(N))

14

The author’s solution is same as sliding window. Instead of maintaining the prefix sum, he calculates it on the fly. Can you explain what part is not clear in the prefix sums one? BTW, do you know what is prefix sum and how it is used?

15

You can see author’s implementation for it.

16

The solution with segment trees should also fit in time limit, though being slower. I went through your code and there was a problem in the query function which can take O(N) complexity as you are not using the fact that sum for range has been calculated and you end up traversing each node till the end/ I suggest you to go through this easy tutorial first: http://se7so.blogspot.com/2012/12/segment-trees-and-lazy-propagation.html and then reimplement the solution using segment trees to get better understanding.

17

Your logic seems complicated and tough to understand. Can you please go through the editorial and understand where your approach is different.

18

The logic is same as author’s solution where instead of maintaining the prefix sums in an array, we calculate them on the fly using sliding window concept.

19

This solution is also in o(1) space complexity and o(n) time complexity. Plzz check it out.
check here

1 Like
20

Thanks for ur approach @gyanendra371

1 Like