PROBLEM LINK:
Author: Devendra Agarwal
Tester: Anudeep Nekkanti
Editorialist: Amit Pandey
DIFFICULTY:
Medium-Hard.
PREREQUISITES:
Dijkstra Algorithm, STL uses.
PROBLEM:
You are given a graph, you need to find the shortest walk in the graph from src to snk which satisfies the following property:
Let the shortest path from src to snk goes from edges E_{1} -> E_{2} -> \cdots -> E_{k} , then Weight(E_{1}) > Weight(E_{2}) < Weight(E_{3}) > Weight(E_{4}) \cdots and so on.
QUICK EXPLANATION:
The given problem can be solved using few modification in Dijkstra Algorithm.
EXPLANATION:
First Subproblem:
Given a graph, You need to find the shortest path in the graph from \text{src} to \text{snk}, without any condition. This problem can be solved using Dijkstra Algorithm. In Dijkstra Algorithm, We initialize distance of the \text{src} with 0, and distance of other vertices as \infty and add \text{src} into a priority queue, and we do it in following manner.
while Q is not empty:
u ← vertex in Q with min dist[u] // Source node in first case
remove u from Q
for each neighbor v of u: // where v has not yet been removed from Q.
alt ← dist[u] + length(u, v)
if alt < dist[v]: // A shorter path to v has been found
dist[v] ← alt
prev[v] ← u
end if
end for
end while
The given pseudo-code calculates the shortest path for each of the vertex. The shortest path for the \text{snk} can be reported easily. Implementation of the Dijkstra Algorithm can be looked here.
Second Subproblem:
You are given a graph, you need to find the shortest wak in the graph from src to snk which satisfies the following property:
Let the shortest path from src to snk goes from edges E_{1} -> E_{2} -> \cdots -> E_{k} , then Weight(E_{1}) < Weight(E_{2}) < Weight(E_{3}) < Weight(E_{4}) \cdots and so on.
In sub-problem 1, we kept a visited array. Once a node has been visited, we get the shortest path for that particular node and there is no need to visit the same vertex again. We can do it in a different manner, at the moment we are exploring vertex v, and pushing all neighbour of v in the priority queue, we can delete all neighbouring edges of vertex v just after pushing them in priority queue.
So, for solving subproblem 2, Consider we have arrived at vertex V by an edge having weight W. when removing the vertex V from the priority queue, push all neighbour X of V if W_{VX} > W, and delete all those edges from the edge-list . This algorithm guarantees that each edge is processed at most once. hence, algorithm will terminate. We may visit a vertex more than once.
The proof of correctness of the given algorithm can be understood in following way. If we arrived at vertex V with cost C_{1}, and later we arrived at same vertex with cost C_{2}, then C_{1} < C_{2}, cost of last explored edge in both cases are the same .
Implementation details:
Preprocess the graph by sorting outgoing edges from each node (by weight). Keep a pointer at each vertex, which will tell edges having higher weight should not be considered.
Original Problem:
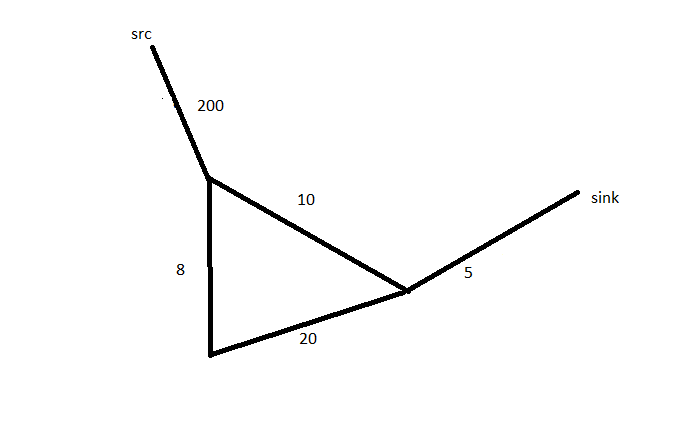
To solve the original problem, where edge length is increasing and decreasing alternatively. We need to make a few changes in second subproblem. We will keep two copies of the graph in as the edge list, Call them GL and GS. A \text{counter} should be kept, \text{even counter} will denote that we are looking for a smaller edge and \text{odd counter} will tell that we are looking for a larger edge than previous one.While we are looking for a larger edges we will delete those larger edges after pushing them in the priority queue.This deletion will happen only in larger copy of the graph which is edge-list GL, and similarly in other case.
The reason for keeping two copies of graph is that if edge E has been taken and it is larger than last one, then later it can considered again(as shorter than last one).
Now see the reason of keeping two copies of graph, edge having length 10 is being considered twice. During execution of the algorithm, first it will be deleted from the smaller copy of the graph i.e. GS(while traversing from length 200 to 10)and later it will be deleted from the larger copy of the graph i.e. GL(while traversing for length 8 to 10).
As the deletion can be costly or can have linear complexity, we can keep counters which will tell range in which edge list need to be considered. Time Complexity of the above approach will be O(ElogE + ElogV), O(ElogE) will appear due to sorting edge list, and O(ElogV) due to Dijkstra.
Solutions:
Setter’s solution can be found here.
Tester’s solution can be found here.
 . Will take care in near future for sure
. Will take care in near future for sure 