Problem Link
Setter: Hasan Jaddouh
Tester: Amr Mahmoud
Editorialist: Bhuvnesh Jain
Difficulty
EASY-MEDIUM
Prerequisites
Strongly Connected Components, Bfs / Dfs
Problem
Find the minimum number of cells to select in a matrix so that we can reach every cell from it through a series of moves which is, “You can move from one cell to another only if they are adjacent (i.e. share a side) and the height of destination cell is not more than height of current cell.”
Explanation
The edges in the graph will be between cells (i, j) and (x, y), only if they share a side. Also, the edges will be directed as the edge exists from a cell into another only if the height of destination cell is not less than the height of the current cell.
For example in the sample input 1, the edges will be as follows:
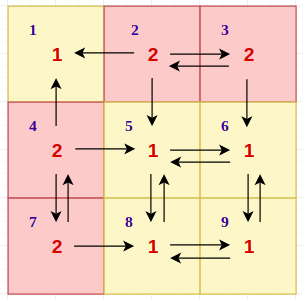
Now given a directed graph, we want to select a set of cells so that all cells are reachable from it. The first observation is 2 decompose the graph into Strongly connected components, as there may be cycles in the graph. This is because all the vertices in a cycle can be visited by starting from any vertex.
Now, we have a directed graph in which there are no cycles. (It is also called a DAG). In this graph, we claim that we chose only vertices with indegree 0 to be in our set as the possible candidate solution.
Reason : Let us say there is an edge P to Q in the DAG. Let us denote the set of vertices reachable from Q to be S. Then all vertices in S are also reachable from P. But P is not reachable from Q. So continuing this process, we will see that only vertices having indegree 0 are not reachable from any other vertex but they as a set cover all the vertices reachable from it.
The DAG of input sample 1 is give below:
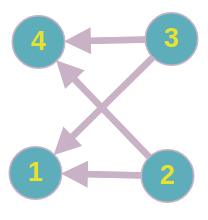
In the above figure, 1 represents the set {1}, 2 represents the set {2,3}, 3 represents the set {4,7} and 4 represents the set {5,6,8,9}.
Thus, the algorithm is as below:
- Construct the directed graph from the grid. Complexity is $O(N * M)$. Also, the number of edges in the graph is bounded by $(8 * N * M)$ as each cell can have at most 4 neighbors and it can have edge in both directions.
- Decompose the graph into one with no cycles. You can use Tarjan's algorithm or Kosaraju algorithm for this step.
- Find the number of vertices with indegree $0$ in DAG.
Author’s Solution
The solution counts the number of components having same heights, such that all adjacent components are less (strictly) than it.
Proof: Each such component consisting of all cells of same height can be represented by 1 cell only. Now, each component can either have all adjacent components less tha it or not. If all cells adjacent to it are smaller, the those can be reached from the current cell, so they are ot counted towards the answer. If we repeat this process, for each component, we are bound to find only those cells which will contribute to the answer. Also, if we assume some cell that shouldn’t be in answer was counted by above process, the it would contradict the fact that all adjacent components are lesser than it.
The above process can be simply implemented by a dfs call from every vertex and check if all components adjacent to it are smaller than it or not. For details, refer to author’s solution.
Time Complexity
O(N * M), per test case.
Space Complexity
O(N * M)

