PROBLEM LINK:
Author: Gaoyuan Chen
Tester 1: Minako Kojima
Tester 2: Shiplu Hawlader
Editorialist 1: Miguel Oliveira
Editorialist 2: Pawel Kacprzak
DIFFICULTY:
HARD
PREREQUISITES:
Max-flow, Graphs
PROBLEM:
You are given N courses and M semesters. X[i][j] is the expected grade which you will get for completing the i-th course in j-th semester or -1 if i-th is not taught in j-th semester.
You are also given K prerequisites. Each one is in form (i, j) and means that course i has to be taken before course j.
Your task is to compute the maximum possible expected average grade if you have to take every course exactly once.
QUICK EXPLANATION:
Model the problem and prerequisites as min-cut / max-flow problem and find a max-flow in it corresponding to the maximum achievable expected sum of grades.
EXPLANATION:
First, let’s ignore the dependencies. The answer is just the maximum grade per course in any of the semesters, which is trivial to compute but let’s put this in another perspective:
For each course, the best grade is 100 - (minimum grade we lose by picking one of the semesters).
To model this as a network flow graph, we do 4 things:
- Create a vertex for each pair (course i, semester j).
- Create a source vertex which is connected to the first semester of each course i by an edge with capacity 100 - grade(i, 1).
- For every semester j from 2 to M, connect the vertices of each course i from semester j-1 to j with capacity 100 - grade(i, j) or 100 if the course is not available (it’s the same as having grade 0, recall that it’s guaranteed there is a solution).
- Create a sink vertex and connect the last semester of each course to it, with infinite capacity.
Consider the following example with 3 courses and 3 semesters:
3 3
10 70 100
80 50 40
80 20 40
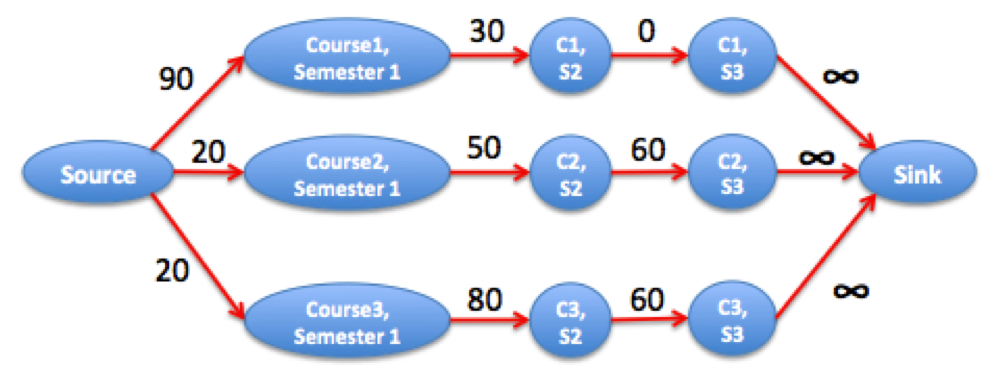
The corresponding graph is depicted in the above picture. The maximum flow is equal to the combined grade loss for all courses. We pick semester 3 for course 1 (zero loss), and semester 1 for courses 2 and 3 (loss 20+20).
The maximum grade average we can get is (N * 100 - maxflow) / N. In this case: (3*100 - 40) / 3 ~= 86.67.
- Returning to the problem, why does this help?
If we model the problem this way, we can also include the course dependencies. Suppose there are dependencies 1->2 and 1->3. The best we can do is course 1 in semester 2 and courses 2 and 3 in semester 3 for (70+40+40)/3 average.
- If there are dependencies 1->2 and 1->3, then courses 2 and 3 can never be done in the first semester.
This implies that the minimum grade loss for courses 2 and 3 is not bounded by its grades in semester 1. This is the same as changing the capacities associated to semester 1 of courses 2 and 3 to infinity.
- Why do we pick semester j for course 1?
The combined grade loss of doing course 1 in semester 2 + courses 2 and 3 in semester 3 is less than doing course 1 in semester 1 + courses 2 and 3 in semesters 2 or 3.
In terms of network flow, this means that
- if we pick semester j = 1, then courses 2 and 3 are not bounded by grade loss in semester 1. To combine the grade loss by picking semester 1, we connect vertex (course 1, semester 1) to (course 2, semester 2) and (course 3, semester 2) with infinite capacity.
- if we pick semester j = 2, then courses 2 and 3 are not bounded by grade loss in semesters 1 and 2. Same as above but connecting (course 1, semester 2) to courses 2 and 3, semester 3.
- picking semester j = 3 is not possible.
The resulting network is the following
We can see that the maximum flow is 150. The best is to distribute the grade loss of course 1 in semester 2, flow 3, among courses 2 and 3 in semester 3. In fact, 70+40+40 = 300 - 150.
To give you another example, consider the input
3 3 2
10 50 100
80 90 40
80 40 70
1 2
1 3
The best we can do course 1 at semester 1 (10) + course 2 at semester 2 (90) and course 3 at semester 3 (70) = 10+90+70. The resulting graph is
We can see that the maximum flow is 130 because in this case, it is better to distribute the grade loss of course 1 at semester 1, the flow 90, among the grade loss of courses 2 and 3 over semesters 2 and 3, respectively.
In a nutshell, we create a graph with N*M+2 vertices and use a standard maximum flow algorithm. The hard part was to realize how to build the network correctly.
Proof sketch:
Since max-flow equals min-cut, we can think of our problem as of finding a minimum cut in the above graph. Let Pi be a path corresponding to i-th course, i.e. the path formed of edges corresponding to i-th course in all semesters. In order to prove the correction of the above construction, we can show two properties of the graph:
- For every 1 <= i <= N, min-cut contains exactly one edge from Pi.
- For every constraint (i, j), if min-cut contains the k-th edge of Pi, then it contains the x-th edge of Pj, where x > k i.e. j-th course is taken in later semester than i-th course.
These two fact can be shown quite easily, but we will omit exact proofs here. Intuitively, if you pick any edge from Pi, then Pi is disconnected and there is no need for taking any other edge from it. Moreover, an edge (i, j) corresponding to a constraint, prevent us of taking course j before course i, because if you did it, then in order to make the graph disconnected, you would have to add the second edge of Pj to min-cut which contradicts the first fact.
AUTHOR’S AND TESTER’S SOLUTIONS:
To be uploaded soon.
RELATED PROBLEMS:
To be uploaded soon.
