PROBLEM LINK:
Author: Kamil Debowski
Tester: Niyaz Nigmatullin
Editorialist: Kamil Debowski
DIFFICULTY:
EASY
PREREQUISITES:
binary search
PROBLEM
0n the two-dimensional plane, there is a shape consisting of a square and an isosceles triangle that satisfy a few given conditions.
The conditions implied that the shape must look like this:
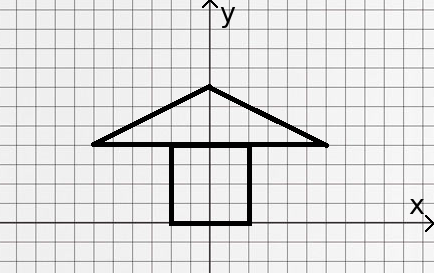
Sides of the square and the triangle could be shorter or longer but generally the shape must be similar to the one from the drawing above.
In particular, the point (0,0) is exactly in the middle of the bottom side of the square.
The problem is interactive and there is nothing given in the input initially.
We can ask queries.
In each query we choose a point with integer coordinates and the system will tell us whether the chosen point belongs to the shape (i.e. it’s inside or on the boundary) or not.
Our task is to find the total area of the shape within 100 queries.
Coordinates can be up to 1000.
EXPLANATION
Let’s assume that we have as many queries as we need.
So for each points with allowed coordinates (up to 1000), we know whether it’s outside or not.
Let’s think how to easily compute the answer (the total area), without hard geometry.
So for example, we know that following points are inside (or on the boundary) of the shape:
![drawing points][1]
To know the side of the square, it’s enough to take a look at points on the x-axis.
The last point on the right is (2,0) so the side of the square must be 4.
We can find the highest point of the triangle in the similar way: there is a point (0,7) so the height of the triangle is 7 - 4 = 3 (remember that the square has side 4).
The last information we need is the base of the triangle.
To compute it, we should find the rightmost point.
In this drawing it is (4,7), so the length of the base of the triangle is 7 * 2 = 14.
Knowing the base and the height of the triangle, and the side of the square, we can easily find the total area.
But we can’t ask so many queries.
Fortunately, we care only about some particular points.
First, we need the rightmost point on the x-axis.
To find it, we can ask about points (0,0), (1,0), (2,0), …, till we get a response “NO”.
Know we know the side of the square (let A denote it).
Similarly, we can ask about points with x = 0 to find the highest point.
The last and trickiest part is to find the righmost point of the base of the triangle (it was (4,7) in the example above).
Fortunately we already know the y-coordinate that it must have!
Earlier we found the side of the square A, and from the statement we know that the bottom of the triangle has the same y-coordinate as the top of the square.
So its y-coordinate must be equal to A.
So we can ask about points (0,A), (1,A), (2,A), … and this way we will find the rightmost point of the triangle and thus the base of the triangle.
The described algorithm needs to iterate over some consecutive points three times.
So it would need up to 31000 queries for coordinates up to 1000.
This approach is enough to solve the first subtask, but not enough for the full score.
To improve it, we can replace iterating over points with the binary search, what reduces the number of queries to about 3log(1000) what is much smaller than 100.
IMPLEMENTATION
In interactive problems it’s useful to write a function to ask queries.
Thanks to that, in the main part of code we don’t have to care about flushing etc.
bool ask(int x, int y) {
printf("? %d %d\n", x, y); // print the query
fflush(stdout); // flush the output
string response;
cin >> response; // read the response from the input (a string "YES" or "NO")
return response == "YES"; // return true if we got "YES"
}</pre>
It’s also good to extract the binary search into another function.
Let’s see a piece of code that considers the sequence of points (0,y), (1,y), …, (1000,y) and finds the last point that is inside the shape:
int findX(int y) {
int x_low = 0, x_high = 1000;
while(x_low < x_high) {
int x_mid = (x_low + x_high + 1) / 2;
if(ask(x_mid, y)) // if this point is inside
x_low = x_mid;
else
x_high = x_mid - 1; // if it's outside, the x-coordinate is too big
}
// now x_low == x_high
return x_low;
}
Likely you will need a similar function to find the y-coordinate of the highest point (the top point of the triangle).
Finally, we can combine everything into the solution:
int half_square_side = findX(0); // y = 0, find biggest x
int square_side = 2 * half_square_side;
int half_triangle_base = findX(square_side); // y = square_side, find biggest x
int triangle_base = 2 * half_triangle_base;
int top = findY(0); // x = 0, find biggest y
int triangle_height = top - square_side;
printf("! %d\n", square_side * square_side + triangle_base * triangle_height / 2);
POSSIBLE MISTAKES
You must remember about characters “?” and “!” before printing a query or the answer, and about flushing the output.
One more thing is that you shouldn’t choose the range of coordinates (in the binary search) to for example 1005 instead of 1000, because it can lead to asking a query about a point with coordinates greater than 1000.
Such a point must be outside the shape obviously, but you will get WA — the statement says that coordinates in queries can’t exceed 1000.
[1]: https://codechef_shared.s3.amazonaws.com/download/upload/LTIME45/RRIIK7T.png
AUTHOR’S AND TESTER’S SOLUTIONS:
Setter’s solution can be found here.
Tester’s solution can be found here.