PWRTREE - EDITORIAL

general
, , , , , ,
1

PROBLEM LINK:

Practice
Contest: Division 1
Contest: Division 2

Setter: Alei Reyes
Tester: Aleksa Plavsic
Editorialist: Taranpreet Singh

DIFFICULTY:

Easy-Medium

PREREQUISITES:

Constructive algorithms, Directed graphs. (Knowledge of Tournament Graphs would be an advantage)

PROBLEM:

Given N vertices and for every pair of distinct vertices, a directed edge is given. Can we remove some of the edges to make this tree a power tree? If yes, Print the edges to be removed from the given complete directed graph to obtain power tree (of any degree).

A power tree of degree l, denoted by PT(l), is a directed graph, defined recursively as:

  • PT(0) consist of just a single node.
  • for l > 0, a new node u is made as root and is connected by a directed edge from u to root of power trees of all degrees smaller than L to power trees of all smaller degrees.

SUPER QUICK EXPLANATION

  • Answer does not exist if N is not a power of 2.
  • Each power tree of degree l can be broken into two power trees of degree l-1 by removing one edge. We will be adding that particular edge for this problem.
  • We can run a knockout tournament type implementation (matching vertices for the match in any way), assigning edge from winning vertex to losing vertex, moving only winning vertex to next level.

EXPLANATION

For this problem, let us rule out impossible cases first, followed by a valid construction with proof.

First of all, Let’s count number of vertices power tree of degree l contains. Assume C(l) means the number of vertices in power tree of degree l.

C(0) = 1 as power tree of degree 0 is a single node.

Power tree of degree 1 contains 1+ C(0) = 2 vertices.

Power tree of degree L contains 1+C(0)+C(1)+C(2) \dots C(L-1) = 1+1+2+4+\dots + 2^{L-1} = 2^L vertices.

So, we see, each power task of degree L contains 2^L vertices.

Hence, there cannot be any valid power tree with N vertices, N not being a power of two, thus, leading to an impossible position since at least one vertex will be left out.

Now, we have N as a power of two. Assume 2^L = N.

Now, the thing about graph given is, that we know there exist an edge for every pair of vertices. It just tells us the orientation of the edge.

The critical observation is that, (crux of the whole problem)

Adding a directed edge from root u of power tree of degree L to root of another power tree of degree L gives a power tree of degree L+1 rooted at u.

See the following images, showing two power trees of degree three. We have vertex 1 and vertex 9 in list currently.

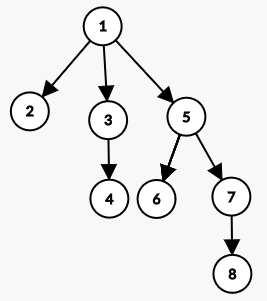
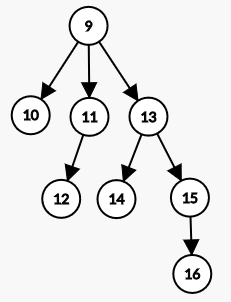
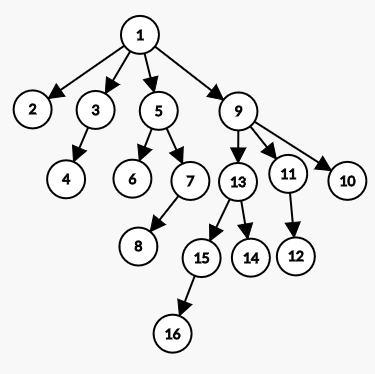
alt text alt text

If the orientation of the edge is from 1 to 9, it results in the following power tree.

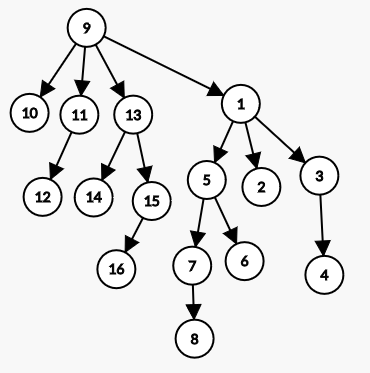
alt text

Otherwise, If the edge is oriented from 9 to 1, it leads to the following power tree.

alt text

Concluding from above, if we merge power trees of the same degree, we can always get power tree of next higher degree, irrespective of the orientation of edges. Orientation will only alter the root of power tree of higher degree. In fact, the source of the edge will become the root of the new power tree.

This proof automatically gives us a construction method.

We will construct the power tree degree wise. Firstly, we have all vertices disconnected, N power trees of degree 0. Make pairs of all vertices and see who wins. Add a directed edge from the source vertex to destination vertex, remove the losing player from the list. Now, we can see that we have N/2 power trees of degree 1. Once again, Make pairs of these vertices randomly (or any way you prefer), see who wins, add directed edge and remove losing vertex.

We repeat this until we obtain only one vertex in the list. Now, the edges not added to our tree are the ones to be removed, Obtaining a power tree of degree L.

Related Notes

First of all, this type of graph is known as Tournament graph, about which, can be read about here. Also, a problem appeared in October Lunchtime 2017 which can be seen here, based on tournament graphs.

Time Complexity

The time complexity for construction is O(N) since we take O(1) time to add an edge, and we add exactly N-1 edges.

But Reading input takes O(N^2) time per test case, which dominates the overall complexity.

Memory Complexity is O(N^2) so as to store input graph per test case.

AUTHOR’S AND TESTER’S SOLUTIONS:

Setter’s solution
Tester’s solution
Editorialist’s solution

Feel free to Share your approach, If it differs. Suggestions are always welcomed. :slight_smile:

1 Like
2

The most crucial observation would actually be that for 2^N vertices tournament graph there ALWAYS exists a power tree (proof by induction), and missing this observation is probably the reason so little people got AC on this easy? problem.

Perhaps an interesting question would be to count number of different power trees, which seems to be fixed formula in terms of N (not depending on orientation of C(N,2) edges).

2 Likes
3

enter code here
t = input()
while(t):
t = t - 1
n = input()
k = [1, 2, 4, 8, 16, 32, 64, 128, 256, 512]
dic = {}
edge = []
for i in range(n * (n - 1) / 2):
a, b = map(int, raw_input().split())
dic[(a, b)] = 0
edge.append((a, b))
if(n == 1 or n == 2):
print 0
elif((n in k)):
l = []
k = []
for i in range(n):
k.append(i + 1)
l.append(k)
while(len(l[-1]) > 1):
a = l[-1]
b = []
for j in range(0, len(a), 2):
try:
c = dic[(a[j], a[j + 1])]
dic[(a[j], a[j + 1])] = 1
b.append(a[j + 1])
except:
dic[(a[j + 1], a[j])] = 1
b.append(a[j])
l.append(b)
print ((n)*(n - 1)/2) - n + 1
for i in range(len(edge)):
if(dic[edge[i]] == 0):
print i + 1,
print
else:
print -1

  • it’s giving wrong ans pls help
4

“Firstly, we have all vertices disconnected, N power trees of degree 0. Make pairs of all vertices and see who wins.”

How are we judging who wins?What does win signify here?

5

The “winner” is determined by the direction of the edge between the two root vertices.

1 Like
6

It is guaranteed that either edge (u,v) is there, or the edge (v,u) present in the graph. We take source as the winner since, in power tree, we need to add an edge from root to other power trees.

1 Like
7

Beautiful problem. I had no idea that reading the editorial and then trying to prove the observations would be so much fun :slight_smile:

8

So you are saying we determine ‘u’ to be winner if there exists an edge (u,v) in the input and then we make a power tree with root at ‘u’.

9

Precisely :slight_smile:

1 Like