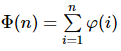PROBLEM LINK:
Author: Pavel Sheftelevich
Tester: Vlad Mosko
Editorialist: Pawel Kacprzak
DIFFICULTY:
HARD
PREREQUISITES:
Math, Number-theory
PROBLEM:
You are given integer N and integer D. Your task is to compute the number of unordered pairs of numbers \{A, B\} such that 1 \leq A, B \leq N and \gcd(A, B) = D.
QUICK EXPLANATION:
First notice that the number of pairs which we are looking for equals the number of co-prime number non-greater than N \mathbin{/} D. Then use Euler-totient function to compute the number of co-prime numbers not-greater than N \mathbin{/} D. In order to pass all testcase, use precomputation of sums of Euler-totient function for some intervals to speed up the real time computation.
EXPLANATION:
The crucial observation here is that the number of unordered pairs of number \{A, B\} not greater than N, for which \gcd(A, B) = D equals the number of co-prime numbers not greater than N \mathbin{/} D. This is true, because if you multiply these co-prime numbers by D, then their \gcd equals D, since they do not share any common prime factors other that prime factors of D.
We just reduced our problem to finding the number of co-prime number non greater than some integer N.
The most straightforward method to do that is to iterate over all possible pairs of number and check if their \gcd equals 1 using Euclid algorithm. This results in algorithm which has O(N^2 \cdot \log(N)) complexity. This allows us to solve the first subtasks, but is a way too slow for higher constraints.
The faster solution uses Euler-totient function which is a very famous function denoted by \phi(N). The value of \phi(N) is the number of positive integers not greater than N which are co-prime with n. It can be computed using factorization. So the number of co-prime number smaller than N equals the sum of \phi(i) for all i \leq N. For more details, I encourage you to read this great topcoder tutorial on prime numbers, factorization and Euler function. But since we have to compute \phi(i) for all numbers from 1 to N, this will time out, because N can be at most 5 * 10^8.
In order to speed up our solution, we can precompute values of sums of \phi of integers not greater than K, 2 K, 3K, \dots, N - K for reasonable chosen K. Author of the problem decides to choose K to be 250000. This allows us to compute \phi for at most K different values and uses the precomputed sum of \phi for smaller values.
The time complexity here depends on K and equals O(K \cdot \log(N) + N \cdot \log(\log(N))), where the first summand is taken from computing \phi for at most K values, and the second is taken from computing prime numbers using in factorization - we can use the sieve in order to do that.
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.