PUPPYCT - Editorial

[admin]

PROBLEM LINK:

Practice
Contest

Author: Pavel Sheftelevich
Tester: Vlad Mosko
Editorialist: Pawel Kacprzak

DIFFICULTY:

MEDIUM

PREREQUISITES:

PROBLEM:

You are given an N \times N grid and K special distinct cells in it. For each of these K cells, let’s say (i, j), we know that all cells which lie on the same diagonals as (i, j) are full of cats.

For example, here are a few diagonals marked on 5 \times 5 grid:

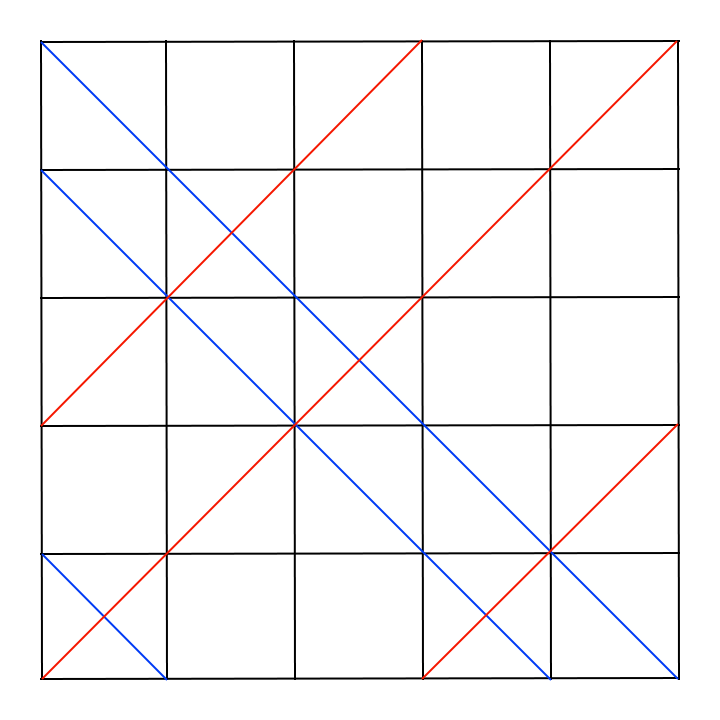
We call blue diagonals left diagonals and red diagonals right ones.

The task is to find out how many cells on the grid are free of cats.

The most straightforward solution is to for each of the given K cells, let’s say (i, j), mark all cells which lie on the same diagonals as (i, j). Since there is always one left and one right diagonal crossing any cell, we have to mark at most O(N) cells for each input cell. At the end we need to subtract the number of marked cells from all cells in the grid. This solution requires total O(N^3) time and might pass some small testcases, but we have to do better.

Let’s enumerate our diagonals first.

Let’s consider any cell (i, j), where i is the row number and j is the column number.

For each left diagonal (a blue one), all cells lying on this diagonal has the same value of i - j. In order to enumerate left diagonals, let’s assign to each one a single integer i - j + N. This allows us to refer to left diagonals by numbers 1, 2, \ldots, 2 \cdot N - 1.

We can make a similar mapping for right diagonals (red ones). Notice that all cells lying on one right diagonal has the same value of i + j. In order to enumerate right diagonals, let’s assign a single integer i + j - 1 to each one. This allows us to refer to right diagonals by numbers 1, 2, \ldots, 2 \cdot N - 1.

This two enumerations are explained further on below drawings:

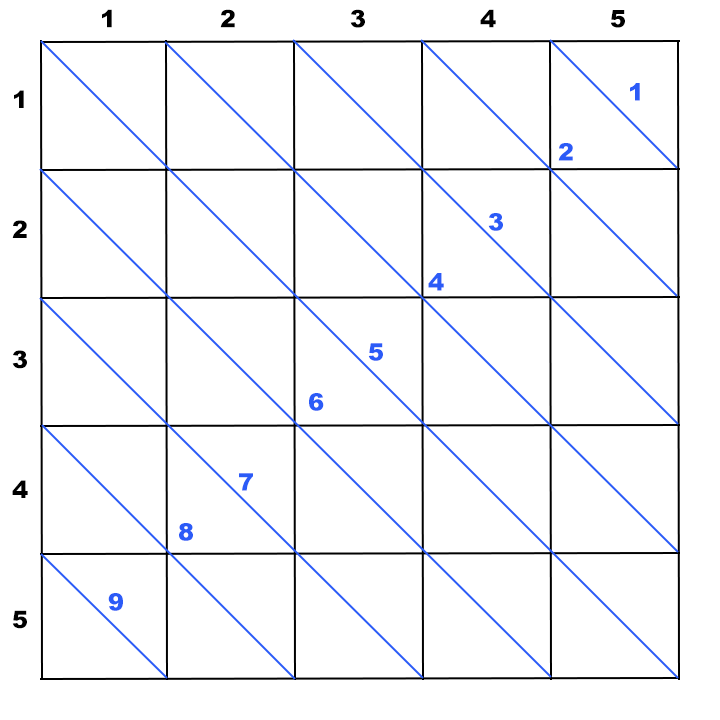
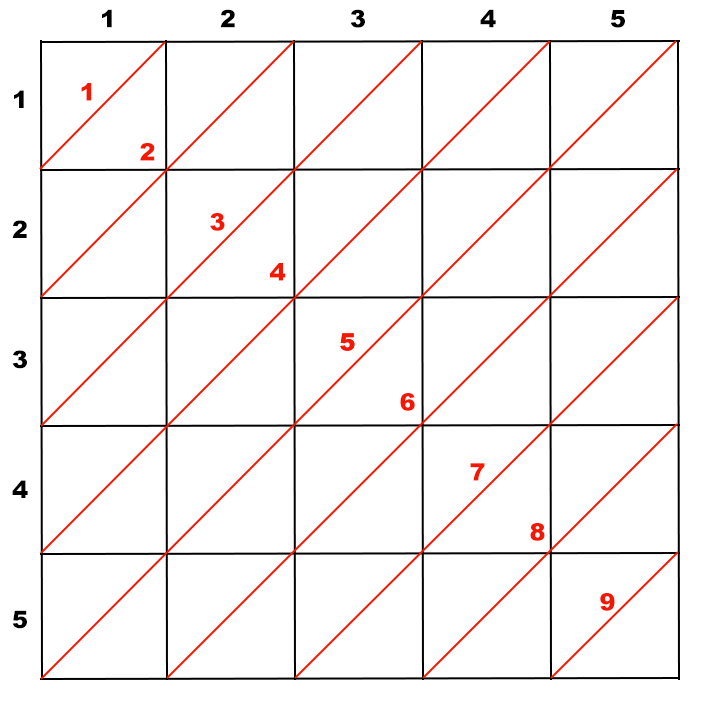
Being able to enumerate the diagonals, while iterating over input cells, we can mark diagonals as occupied by cats. In order to do that, for each input cell, compute the index of left and right diagonals which crosses it and mark them as occupied by cats.

To get the result, we can iterate over all grid cells and for each one, we check if any diagonal crossing it is occupied by cats. The result is the number of cells for which no one of two diagonals crossing it is occupied by cats. This solution has time complexity O(N^2) and while it allows us to solve more testcases than O(N^3) solution, it is still to slow to pass all tests.

Since N can be as big as 10^6, we have to avoid iterating over all grid cells, if we want to speed up our solution. Notice that, if we are able to count the number of cells occupied by cats, we can easily get the result by subtracting this number from N \cdot N - the total number of cells. The first step here is the same as in the O(N^2) method - we iterate over input cells marking diagonals which are full of cats.

From now we refer to diagonal as a diagonal which is marked as being full of cats.

Notice that we can easily get the number of cells crossed by a diagonal (left or right), if we know the number assigned to this diagonal. In our case, we can use the equation below to get the number of cells crossed by a diagonal (both left and right) for a given id number assigned to diagonal:

cellsCrossedByDiagonal(id)= \begin{cases} id, &\text{if } id\leq N\\ 2 \cdot N - id, & \text{otherwise} \end{cases}

Based on the above equation, we can iterate over all diagonals and count the total number of cells in these diagonals. Let T be that number.

Everything looks fine right now, but we might take into account too many cells. For example, a left and a right diagonal may cross each other, and we count this crossed cell exactly two times in T. In order to get the final result, we have to subtract the number of cells which are crossed by two diagonals full of cats from T.

How to get the number of cells which are crossed by two diagonals? Notice that a left diagonal cannot cross another left diagonal. This is true for right diagonals also. So for each right diagonal, we want to get the number of left diagonals which cross it.

If you take a closer look at a right diagonal with number K assigned to it, you will notice that it crosses some left diagonals with even numbers assigned to them if and only if K is even too. Otherwise it crosses some left diagonals with odd number assigned to them.

Let K be a number assigned to a right diagonal, then if K \leq N, it crosses all left diagonals with numbers in range [N - K + 1, N + K - 1] with the same parity as K.

Otherwise, if K \gt N, let X = 2 \cdot N - K. Then this diagonal crosses all left diagonals with numbers in range [N - X + 1, N + X - 1] and same parity as K.

So the only thing to do is to get the number of diagonals with even/odd numbers assigned to them is some range [A, B] which are full of cats. How to do that? Well, we can use prefix sums to do that. Precisely, compute the number of diagonals with even/odd numbers assigned to them in range [1, B] for each 1 \leq B \leq 2 \cdot N - 1. Let oddPrefix** and evenPrefix** represent this prefix sums. Then in order to get the number of, let’s say odd, diagonals which are full of cats in a range [A, B], we just compute oddPrefix** - oddPrefix[A - 1].

The total complexity of this method is O(K + N), because in the first step, we iterate over all input cells and in the second step we iterate a few times over all diagonals, and there are O(N) diagonals.

AUTHOR’S AND TESTER’S SOLUTIONS:

Author’s solution can be found here.
Tester’s solution can be found here.

[saurabh_29]

nice editorial

[archazey]

I didn’t read the whole editorial but it seems like my ideea. I thought to count the number of cats for blue diagonals first,then for every red diagonal I counted length of diagonal-how many blue diagonals I encounter.
For that you can make partial sums for odd and even diagonal,but there are some cases and the pointers killed me xD.
Nice ideea but the implementation for 100 pts isn’t nice…

[a]

@archazey.: The editorial is fine. But can you tell me

Let K be a number assigned to a right diagonal, then if K≤N, it crosses all left diagonals with numbers in range [N−K+1,N+K−1] with the same parity as K.
Otherwise, if K>N, let X=2⋅N−K. Then this diagonal crosses all left diagonals with numbers in range [N−X+1,N+X−1] and same parity as K.

How did you come to this formula? From observation or some logic or function or intuition?

I also want to request others to post their own thought processing if possible?

[archazey]

a____: At first I didn’t thought much about solution (like every detail),just the main ideea.And when I encountered the problem with counting the intersecting diagonals, I saw that there are 2 types(like in a table of chess -white and black or odd and even,how u want to call them), then I also saw that for a length of one diagonal,it intersects in rage [middle-x,middle+x],with some cases.
These are just observations,seen from some drawings,I really don’t know what I could have done if no solution came up…
I cannot find other simpler solution…

I solved some time ago a problem where there are some points in a grid of size NxN with some occupied cells and for a query with a given points (x,y) and a size Z u need to count how many occupied cells are there in the diamond of top cell (x,y) and line length Z.
The best solution was to make some partial sums on diagonals,and it was killing u,I personally didn’t like the implementation. Also it was a solution with partials sums on 4 types of triangles,which was pretty ok.

I just wanted to admit that for this type of problems MAYBE u can find something really easy to implement

[a]

archazey.: Thanks for your answer…what do you mean by [middle-x,middle+x].can you please give the problem link/explanation?

[archazey]

I mean the number of diagonals of some type(white or black).
It is pretty hard to explain,if you do some drawings you’ll see more clearly
Look on my code if u wanna really know how to implement this problem.

[pkacprzak]

I am the editorialist here. While I was solving the problem, I came up with this enumeration of diagonals first (originally it was just i - j for left diagonals and i + j for right, but I changed it to be in range [1, 2n - 1]). Then, as soon as I realized that, let’s say right, diagonal crosses some left diagonals, I checked up which ones it crosses and it turned out to be this formula which I proposed. According to your question, it was observation, but if you take a closer look at the enumeration of diagonals, you will see also why this works

[a]

Thank you very much…I now understand the whole idea.

[pkacprzak]

That’s cool The problem was really interesting.

[yougaindra]

I am not able to understand the last paragraph (the one just before complexity analysis). Can somebody explain how does it work?

[jeffrycopps_2]

@pkaprzak,
please explain the last paragraph with an example.
So the only thing to … we just compute oddPrefix**−oddPrefix[A−1].

[pkacprzak]

The concept used here is called prefix sums. For example, if you are given an array of n integers [a1, a2, …, an] and you want to quickly compute the sum of any subarray of these array, you can do it in constant time and O(n) preprocessing. Let prefix[1…n] be an array for which prefix[i] = a[1] + a[2] + … + a[i]. You can compute the whole prefix array in O(n) time. Do you see it? Then the sum of integers with indices from i to j equals prefix[j] - prefix[i - 1], because you can take prefix[i] and cancel out all integers before j. Is it more clear now?

[jeffrycopps_2]

I am fine with prefix sums. But how the left and right diagonals are related with prefix sums. Or how odd and even diagonal indexes are related with prefix sums is my question. Can you please explain for a 5x5 matrix having (1,2) (2,2) dumps.

[pkacprzak]

Basically, any right diagonal crosses some left diagonals with even/odd numbers is some range [a, b]. Normally, we can count the number of these diagonals by examining the range [a, b] iterating over it, but this is too slow here, so we use prefix sums for this.