PROBLEM LINK:
Author: Prakhar Gupta
Tester: Madhav Sainanee
Editorialist: Prakhar Gupta
DIFFICULTY:
EASY-MEDIUM
PREREQUISITES:
Trigonometry, Basic Geometry
PROBLEM:
Given N points, find out the minimum perimeter of the rectangle with the slope of one of its sides as M such that it covers all the points.
EXPLANATION:
Since the sides of a rectangle are parallel, we can determine both the slopes as m_1 = M and m_2 = -1/M, since m_1m_2 = -1.
For every point, we find out the intercept of the line with slope m_1 passing through (x, y) on the y axis as c_i = y_i - m_1x_i.
The minimum width of the rectangle will come from the points with maximum and minimum c_i.
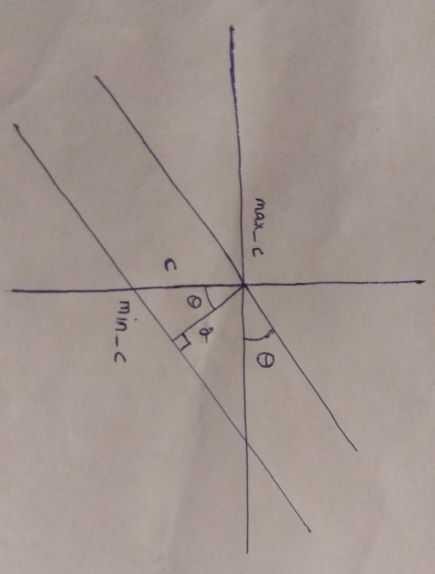
From the figure, c = c_{max} - c_{min} and d, the width of the rectangle, is d = c \times \cos \theta.
Since m_1 = \tan \theta, we can find \cos \theta = \frac {1} {\sqrt{1 + m_1^2}}. Therefore d = \frac{c}{\sqrt{1+m_1^2}}.
Similarly, we can find the length l from the second slope, m_2.
The perimeter is finally 2 (l + d).
There is a special case when M = 0, in which we can’t find the second slope as -1/M. In this case, the rectangle is parallel to the coordinate axes, and the perimeter is 2 (x_{max} + y_{max} - x_{min} - y_{min}).
Complexity: The time complexity is O(N) per test case.
ALTERNATE SOLUTION:
This problem can also be solved by rotating the axes by \theta = tan^{-1}(M) and following the procedure of M = 0 in the normal case, with the new coordinates of the points in the rotated axes.
You can read more about the rotation of axes here.
Complexity: The time complexity is O(N) per test case.
AUTHOR’S SOLUTIONS:
Author’s solution can be found here.
Rotation of axes solution can be found here.