PROBLEM LINK:
Author: Adury Surya Kiran
Tester: Mugurel Ionut Andreica
Editorialist: Lalit Kundu
DIFFICULTY:
Medium-Hard
PREREQUISITES:
advanced maths, geometry, recurrences
PROBLEM:
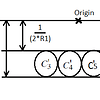
We are given radius of circles C_1, C_2, C_3 and C_4 in the following image:
Now, we are going to draw circles C_5, C_6 and so on in such a way that C_n touches circles C_1, C_2 and C_{n-1}. Like as shown in the following image:
Given upto 10^7 values of n, find sum of radius of circle C_n for all n.
QUICK EXPLANATION:
========================
Using Descartesā Theorem, if we have 3 existing circles of curvature(inverse of radius) a_1, a_2, a_3, we can draw a 4^{th} circle of curvature a_4, touching all three circles such that a_4 = a_1 + a_2 + a_3 \pm 2 \sqrt{a_1*a_2 + a_2*a_3 + a_1*a_3}, where a_4 is negative if it represents a circle that circumscribes the first three.
Now, n^{th} circle in our problem is formed by finding the 4^{th} circle touching circles C_1, C_2 and C_{n-1}. So, we can define our recurrence, solving which we get general term for the radius of n^{th} circle.
EXPLANATION:
================
One of the ways to solve this problem is via Descartesā Theorem. First, lets define what curvature of a circle is.
The curvature of a circle with radius r is defined as \pm \frac{1}{r}. The plus sign here applies to a circle that is externally tangent to the other circles, like the red circle is externally tangent to the three black circles in the image. For an internally tangent circle like the big red circle, that circumscribes the other circles, the minus sign applies.
Descartesā Theorem states that if four circles are tangent to each other at six distinct points, and the circles have curvatures a_i (for i = 1, ..., 4), then:
(a_1+a_2+a_3+a_4)^2=2(a_1^2+a_2^2+a_3^2+a_4^2).
When trying to find the radius of a fourth circle tangent to three given kissing circles(circles that touch each other mutually), the equation is best rewritten as:
a_4 = a_1 + a_2 + a_3 \pm 2 \sqrt{a_1*a_2 + a_2*a_3 + a_1*a_3}
The \pm sign reflects the fact that there are in general two solutions. One solution is positive and the other is either positive or negative; if negative, it represents a circle that circumscribes the first three (as shown in the diagram above).
Now, letās see how we employ this theorem to find solution to the problem.
We know that C_n(for n \ge 4) is formed as a 4^{th} circle tangent to three kissing circles C_1, C_2 and C_{n-1}, where C_1 is being touched by all circles internally. And also, the circle C_n will touch all other circles externally, so we are interested in positive curvature of C_n. And, curvature of C_1 is -\frac{1}{r_1}.
So, we can write using Descartesā Theorem that a_n = a_1 + a_2 + a_{n-1} + 2 \sqrt{a_1*a_2 + (a_2 + a_1)*a_{n-1}}. Now, we can employ this recurrence to find n^{th} circle, in O(n). This will be enough to pass subtask 1.
For subtask 2, we need a constant time solution for each n, that means we need to arrive at a closed form of the n^{th} term of recurrence. Letās see how we can solve this recurrence. Basically, our recurrence is:
a_n = c_1 + a_{n-1} + 2 \sqrt{c_2 + c_1 a_{n-1}},
where c_1 = a_1 + a_2 and
c_2 = a_1 * a_2
Here, we substitute x_n(a new recurrence) as \sqrt{c_2 + c_1 a_{n}}, which implies that
a_n = \frac{x_n^2 - c_2}{c_1} --------Eqn (1)
So, our recurrence is now a_n = c_1 + a_{n-1} + 2 x_{n-1}. In this equation, substitute a_{n-1} and a_n using equation 1 to get,
x_n^2 = x_{n-1}^2 + 2c_1x_{n-1} + c_1^2, which is basically x_n^2 = (x_{n-1}+ c_1)^2. Now, this has greatly been simplified to x_n = x_{n-1} + c_1, whose general term can be written as x_n = nc_1 + C, where C is an arbitrary constant, which depends on x_1.
Now, to find a_n we substitute general term for x_n in equation 1, which yields a_n = \frac{(nc_1 + C)^2 - c_2}{c_1}.
Now, we know the value of a_3 as \frac{1}{r_3}, so we can find value of C by substituting n as 3 in the general form of a_n. As you might note, it will give us two values for C because its a quadratic in C, so, we take the value which gives us correct value for a_4 whose value we already know as \frac{1}{r_4}.
Now, our solution for a single n is constant time.
ALTERNATE SOLUTION:
========================
There is another solution using the concept of inversion of a plane. Letās see this concept in detail.
We are going to transform all points in an x-y plane(say plane 1) to another x-y plane(say plane 2). For each point (x, y) in plane 1, we map it to \frac{x}{r^2}, \frac{y}{r^2}, where r is distance of point (x, y) from origin i.e. \sqrt{x^2 + y^2}. If we consider point (x, y) in polar coordinates as r e^{i \theta}, then we map it to \frac{1}{r} e^{i \theta} in the plane 2. Transformation from plane 2 to plane 1 is simple, we just have to apply the same transformation again for all points in plane 2.
Now, letās see how it affects simple figures: circle and lines. Here I am going to summarise the results, you can easily derive these results by considering equations of lines and circles(doing in polar coordinates will be easier).
-
All the circles which pass through origin in plane 1 will be mapped to straight lines in plane 2. A circle with center at (r, 0) and radius r will be mapped to line x = \frac{1}{2 r} in plane 2.
-
All the straight lines which do not pass through origin in the first plane will be mapped to circles which pass through origin in the second.
-
All the circles which do not pass through origin in the first plane will be mapped to some other circles in the second plane.
-
All the straight lines which pass through origin in the first plane will be mapped to the same lines in the second. Also, note that if there are two points on such a line where one point is at a distance r_1 from origin and another at distance r_2, where r_2 \gt r_1, then distance between them in plane 1 is r_2 - r_1 and distance between these points in transformed plane will be \frac{1}{r_1} - \frac{1}{r_2}.
Now, letās see how we employe this transformation to solve our problem. First, weāll choose a suitable origin in plane 1(plane where all our circles are present). Now, we see that all circles are tangent to circles C_1 and C_2 and we remember that we can transform circles passing through origin to straight lines, so, we choose the point where C_1 and C_2 touch as the origin. Now, we also assume that their centers lie on y-axis at points R_1 and R_2 respectively.
Now if we transform the plane, then circles C_1 and C_2 will become straight lines which are parallel to each other. All the circles C_3, C_4, C_5 \cdots will become some other circles in the transformed plane. But the fact that they all are touching C_1 and C_2 before transformation means that they all touch the two straight lines which are parallel to each other after transformation, which makes all their radii equal in the transformed plane(this radius is equal to \frac{1}{4R_1} - \frac{1}{4R_2}). See the following figure.
So, the equations of lines C_1^{\prime} and C_2^{\prime} are y = \frac{1}{2 R_1} and y = \frac{1}{2 R_2} respectively.
Now, to find the radius of any n^{th} circle in plane 1, we first find coordinates(in plane 2) of two points on the circle and we transform these points back to plane 2 and get the distance between them as the diameter.
We already know the y-coordinate of the centre of circles C_3^{\prime}, C_4^{\prime} and so on. We need to find their x coordinate now. If we have x-coordinate of the center of circle C_3^{\prime}, then we can easily find centre of any circle and we already know the radius of circles in plane 2, so we can also find the coordinates of a point on the circumference, which weāll transform back.
Letās see how we find x-coordinate of center of C_3^{\prime} in plane 2. Keep referring to image below while reading this for more clarity. We know that a line passing through origin in plane 1 remains same in plane 2, so we draw a line Z_1 in plane 1 passing from origin and center of circle C_3. Now, this line in plane represented as Z_1^{\prime} will also pass through center of circle C_3^{\prime} and origin of plane 2. If we know distance of center of C_3^{\prime} from origin somehow, we can calculate its x-coordinate also, since we already have y-coordinate.
We now, try to relate distances in plane 2 with distances in plane 1. Say, the distance d = distance between origin and center of C_3^{\prime}. So, circle C_3^{\prime} cuts line Z_1^{\prime} at two points, distance between these points in plane 1 must be the diameter of C_3 i.e. 2R_3 because the same line intersects circle C_3 at same two points. Distance of these two points from origin in plane 2 can be written as d - r_3^{\prime} and d + r_3^{\prime}. Now, if we transform them to plane 1 and see distance between them, we can say that:
2 r_3 = \frac{1}{d - r_3^{\prime}} - \frac{1}{d + r_3^{\prime}}
In above equation, we can find the d as all other variables are known. And using value of d we can find x-coordinate of center of x_3^{\prime} = C_3^{\prime} as \pm \sqrt{d^2 - y^2}. So, center of n^{th} circle will be x_3^{\prime} + 2(n-3)R_3 or x_3^{\prime} - 2(n-3)R_3, we can now check which one to use by finding radius of C_4 and match with given value in input.
Now, our problem is solved. You can do the calculations yourself to find the closed formula.
COMPLEXITY:
Constant per query.
I canāt understand the logic behind giving tasks of āenter statement to Google and copy-paste formula from thereā kind. It isnāt even useful for ACM ICPC skills - I have strong doubt that solving such task does not affect problem solving skills at all.
ā¦though the recurrence relation u guys made was easier to solve than this one.