I was solving one assignment and I am not getting ideas for this, I tried thinking in terms of dp but couldn’t think of optimal substructure. It goes like this :-
I need to find a minimum number of square tiles of dimension less than the dimension of floor given needed to tile that floor, example:-
- for a floor of dimension n=4 we have tiles of size 1, 2, 3. so 4 tiles of 2*2 will do, I suppose that is minimum;
- Another thing is we may have any number of non-optimal solution to this problem, say for n=4 we may have a tile of 3by3 and 7 tiles of 1by1 i.e. total 8 tiles. I also need to count the number of non-optimal unique solutions (ie. same configuration should not be counted twice).
I am attaching a scerenshot for clarity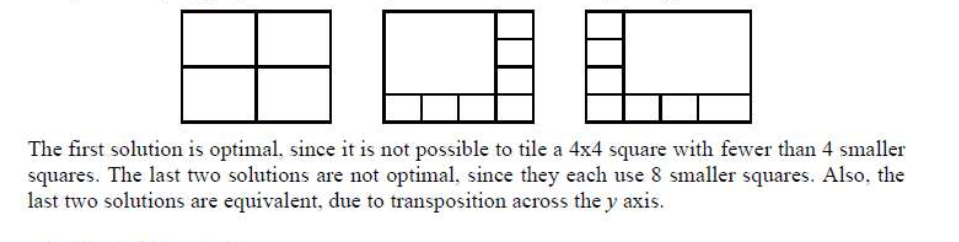
Any help is appreciated…
The 3*3 tile can be placed at any of 4 corners.
They have to be counted same or different?
I am guessing they are same.
@prakhariitd I have edited the problem, please see it.
@vijju123, did you delete the whole answer?
Yes. I am unable to understand the Q, so I decided its better not to cause confusions.
1 Like
what part of question you did not understand ?
Nevermind, I get the Q. Sorry, I cant help in this one bro. (And lol, I am feeling like “why did I wrote that answer in first place”. God! This is what mid-sem exams does to a poor guy like me XD. Sorry for whatever nonsense I might have babbled, lets say, I was not under the best mindset yesterday.
Well, it is an assignment.
2 Likes
Lol. Nailed it dude XDDD. I was like, preparing for tomorrows exam and I read it and I was like “LOL XDDD”. (PS: No offence to anyone intended. Just telling that this thing cracked me up XD)
Before asking for help in Assignments, show us what you have done till now in achieving your goal.
Asides that, I think the answer will always be 4 in case the edge is even. Didn’t think about the case when edge will be odd.
1 Like
does that mean that if somebody can’t solve an assignment, then they can’t ask also.
I have updated the problem, I have tried in terms of dp but could not think of an optimal substructure, What can one I when I don’t have an approach. For even part it seems alright, but it is the case of prime numbers where the main problem lies.
and I see you have not said anything about the earlier answer you gave @prakhariitd. you can let me know if I have not correctly understood your answer.
Prime numbers or odd numbers in general?
well I think as utkarsh1997 said that in case of even length edge it will be 4 as it can be symmetrically divided by the tiles half it’s edges length.
And In case of odd edge length tile I think it should be 4+floor(n/2)2
that is because it can be divided into 1 tile of size ceil(n/2), 3 tiles of floor(n/2) and 2 floor(n/2) tiles of edge size 1 I think thats the only way we can divide tiles minimally.
Let me know if you can divide with less tiles than I showed.
@vijju123 glad it could made you laugh in stress time 
@paras17jain, I feel that merely a formula won’t do your formula does not satisfy for n=7, your answer says 10 but I can fit this into 9 tiles
of sizes 4 , 3 ,3 . 2, 2, 2 , 1, 1 , 1, I will post a diagram later , try fitting these tiles.
1 Like
Hulk, try this and tell if this formula yields correct result for optimal solution-
Let n be dimension of square floor-
For even numbers-
gcd(n,n)=n/2 (since n is excluded)
Ans = (n x n)/[n/2 x n/2] = 4.
For Odd NON-PRIME numbers-
Let k be gcd of n, such that k*l = n.
Try this formula-
Number of squares = 1+ [ n x n - [k x (l-1)]^2 ]/(k x k)
For n=9, this gives-
No of squares = 1+ (81- [3*2]^2 )/9
= 1+ (81-36)/9
=1+5
=6.
FOR ODD PRIME NUMBERS-
Number of Squares follows a pattern-
3-6
5-8
7-9
11-11
13-12
Pattern is +2,+1,+2,+1 (+2 if n+1 is divisible by 4, else +1 )
Check it with your results, I am not that good at finding minimum number of X lol.
(PPS: Mid sems ended today, WEW. Some time for coding now :3 )
Assuming gcd does stand for Greatest Common Divisor, gcd(n,n)=n. How can it be n/2?
excluding n. My bad, I mentioned it in my prev ans. I meant gcd among the numbers available.

