PROBLEM LINK:
Author: Roman Rubanenko
Tester: Mahbub
Editorialist: Jingbo Shang
DIFFICULTY:
Medium
PREREQUISITES:
Dynamic Programming
PROBLEM:
Given a N * M matrix mat with some obstacles inside, deal with Q queries of finding the maximum empty submatrix in the submatrix mat[Li…Hi, *].
EXPLANATION:
First of all, we need to know how to deal with a single query. It is a classical dynamic programming problem, such as POJ 3494 Largest Submatrix with All 1’s. We can maintain an array up[1…N][1…M], where up[i][j] stands for the number of consecutive empty entries starting from (i, j) (inclusive). This array can be generated by the formula as following in O(NM) time.
if mat[i][j] is an obstacle:
up[i][j] = 0
else
up[i][j] = up[i - 1][j] + 1
To find the maximum empty submatrix, we only need to consider the extremal submatrix as shown in the following figure.
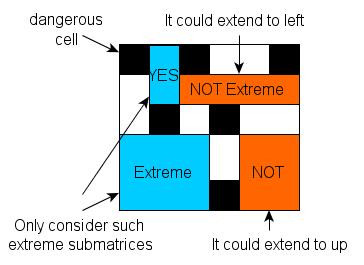
That is, the candidate (extremal) submatrix can’t extend itself in any directions. Extend means to enlarge the submatrix by adding an empty row or column to four directions (left, up, right, down).
Suppose the matrix is bound by the vertical line based on (i, j), its height should be up[i][j] and what we need is to calculate the horizonal boundary (left[i][j], right[i][j]), left and right are both exclusive. Because left and right are similar, we only focus on the left here. By the definition, left[i][j] is the first column k on the left side of j, such that up[i][k] is smaller than up[i][j]. There are two ways to calculate the left[i][li].
[/li]
First one, using the similar way to the disjoint set:
for i = 1 to N do {
for j = 1 to M do {
left[j] = j - 1;
while (left[j] > 0 && up[i][left[j]] >= up[i][j]) {
left[j] = left[left[j]];
}
}
}
This algorithm is O(NM alpha(M)), where alpha() is the inverse of the Ackermann function.
The second one is to use the monotonic stack (up[i][stack[ptr]] > up[i][stack[ptr - 1]] ) to solve this problem in O(NM) time.
for i = 1 to N do {
top = 0;
for j = 1 to M do {
while (top > 0 && up[i][stack[top - 1]] >= up[i][j]) {
top = top - 1;
}
if (top == 0) {
left[i][j] = 0;
} else {
left[i][j] = stack[top - 1];
}
stack[top] = j;
top = top + 1;
}
}
Till now, with the help up, left and right, we can easily deal with a single query in O(NM) time (take all extremal empty submatrix and find the maximum). It is the time to start to deal with the orignal queries.
It is worth noting that, even for the query with L, H restrictions, we only need to consider the extremal submatrix too. Because if the best submatrix can extend in any direction (extend means adding an empty row or column to four directions to enlarge the “best submatrix”), the new area will not be worse after we extended that submatrix even if the extended parts are not in the query boundary.
Let’s define some auxiliary variables. Let c[l][r] is the maximal width of empty rectangle between l-th and r-th rows such that height is r - l + 1.
Initially, c[][] = 0. And then, for each non-obstacle entry (i, j), we update the extremal submatrix to their exact boundaries, as following:
c[i - up[i][j] + 1][i] = max{ c[i - up[i][j] + 1][i], right[i][j] - left[i][j] - 1 }
Finally, we extend the exact boundaries to their inner ones.
c[l][r] = max(c[l][r], c[x][y]), (1 <= x <= l <= r <= y <= N)
we can update c[][] in O(N^2), as following:
for len = N downto 2 do {
for l = 1 to N - len + 1 do {
r = l + len - 1;
c[l + 1][r] = max{c[l + 1][r], c[l][r]};
c[l][r - 1] = max{c[l][r - 1], c[l][r]};
}
}
Similarly, we define d[l][r] as answer for corresponding query. The answer is max{c[i][j] * (j - i + 1), d[i][j - 1], d[i + 1][j]} (the bounary case is d[i][i-1] = 0). So, we should fill in the d[][] in order of increasing the length of interval j - i + 1, in similar way to that we get c[][].
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution will be uploaded soon. here and here.


