LINEPROB - Editorial

editorial
, ,
1

PROBLEM LINKS

Practice
Contest

DIFFICULTY

EASY

PREREQUISITES

Simple Math

PROBLEM

On a standard 2D grid, you draw a line between two lattice points, (x1, y1) and (x2, y2) respectively.

You wish to find the number of grid cells that the line crosses over. Ignore the grid cell if the line never actually enters inside the cell.

EXPLANATION

Without loss of generality we may assume that

x1 < x2 AND y1 < y2

Imagine that the line is actually a ray directed from (x1, y1) to (x2, y2); or from the bottom-left point to the top-right point. Let us take a non-trivial example and break the problem apart.

910×908 15.8 KB

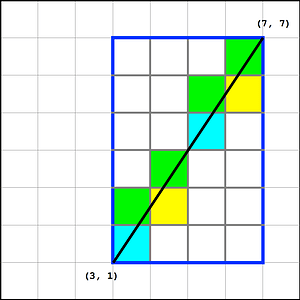
The image above extends the sample the problem statement has, a little bit further. It also offers some valuable insights

The smallest subproblem

The problem can be split into many subproblems. Each of these subproblems exisst for a line segment of the same length, embedded within a rectangle of the same dimensions.

But how do we know how many subproblems can we split the main problem into?

Insight 1
Everytime the ray touches a lattice point, a new smallest sub-problem may be built.

This can be seen in our example above. The line enters at the exact same angle in both the Cyan colored cells. Of course, the shape of the regions of cells the line goes through between consecutive lattice points will be exactly the same. So will be, the number of cells that the line goes through.

Insight 2
The problem can be split into exactly GCD(x2-x1,y2-y1) smallest subproblems.

From Insight 1, we know that we wish to know the number of lattice points the ray touches after starting from (x1, y1). Let

Dx = (x2 - x1)
Dy = (y2 - y1)

x = x1 + Dx * t
y = y1 + Dy * t

We wish to find (x, y) which are integers for all

t ∈ (0, 1]

t must divide both Dx and Dy. Since Dx and Dy are integers, t cannot be irrational. So let us assume that

t = p / q

q must divide both Dx and Dy. For this, q must be a common divisor of Dx and Dy. In fact, we only need to consider the greatest common divisor of Dx and Dy. (For all other values of q, we can always multiply both p and q with a constant and the denominator will be the GCD of Dx and Dy - hence, it will be a redundant value of q to consider)

Thus

q = GCD(Dx,Dy)
p = [1, 2 .., q]

To summerize, there are only GCD(Dx,Dy) smallest subproblems.

Solve the smallest subproblem

Now we are assured that the ray will not cross any other lattice points except the first and the last on its path. The only events the ray may enounter on its journey are

  • cross a horizontal grid line
  • cross a vertical grid line

Insight 3
The ray can never cross the same grid line twice.

Insight 4
The ray enters a new cell everytime it crosses a grid line.

Note in the image above

  • The ray enters the cells filled with Green when the ray crosses a vertical grid line
  • The ray enters the cells filled with Yellow when the ray crosses a horizontal grid line

Thus, we have a one by one mapping to the cells the ray enters, and the grid line the ray crosses. This means that we can simply add up the number of grid lines in a subproblem to calculate the number of cells the ray touches.

Hence the number of cells the ray touches in a subproblem is

(Dx - 1) + (Dy - 1) + 1

Dx = difference in x-coordinate in subproblem
Dy = difference in y-coordinate in subproblem
  • (Dx - 1) is the number of horizontal grid lines in the subproblem
  • (Dy - 1) is the number of vertical grid lines in the subproblem
  • 1 accounts for the initial cell the ray is in.

If you’re wondering why this simple insight won’t apply to the complete problem, consider the anomaly that when the ray crosses a lattice point, it crosses two grid lines, but enters only one new cell. That is why, we first break everything to a subproblem where this cannot happen.

Solve the problem

The answer can be calculated by the following pseudo-code.

Dx = x2 - x1
Dy = y2 - y1

G = GCD(Dx,Dy)

dx = Dx / G
dy = Dy / G

answer = ((dx - 1) + (dy - 1) + 1) * G

Thus, the answer can be found in constant time.

CODE COMMENTARY

There is a glorious pitfall left open for unaware participants.

The problem does not put any constraints on Dx and Dy. What if one of them is 0?

The GCD in this case is still well defined. The answer is well defined as well. If you follow the above calculation closely, you will automatically get an answer of 0. But you should be careful about your implementation.

SETTER’S SOLUTION

Can be found here.

TESTER’S SOLUTION

Can be found here.

6 Likes
2

Once you know how many lattice points exist it is just a simple application of principle of inclusion and exclusion which follows from the insights listed in the editorial. (Note: What I write here is a mere re wording of the editorial solution this is not a different approach)

Just consider the case when the bullet exits a cell. Every time the bullet exits a cell it crosses a vertical or horizontal line or both (and the converse also holds). Except when exiting through lattice points the bullet exits a cell either through a vertical line or a horizontal line but not both.

So in a given grid of axb size the answer is simply no. of times the bullet crosses vertical lines + no. of times the bullet crosses the horizontal lines - no. of lattice points.

Given the trajectory of the bullet it crosses the vertical lines exactly ‘a’ times and the horizontal lines exactly ‘b’ times. So the answer is simply a+b-gcd(a,b)

7 Likes
3

I do not understand that

Dx = (x2 - x1)
Dy = (y2 - y1)

x = x1 + Dx * t
y = y1 + Dy * t

Please help me!!
Why have we written it like this , it is quite non striking for me !
Morover,the next statements are unclear.
I just need to know how to calculate the number of Integral points through which the line segment passes.