PROBLEM LINK:
Author: Praveen Dhinwa
Testers: Istvan Nagy
Editorialist: Praveen Dhinwa
DIFFICULTY:
medium-hard
PREREQUISITES:
geometry, circle related geometry operations like finding the intersection of two circles, tangents of circles.
PROBLEM:
You are given a square with side length 2*L. The coordinates of its vertices are at (-L, -L), (L, -L), (L, L) and (-L, L). You are also given N disks (each disk is opaque, and light rays cannot pass through them) each of radius R. The centers of each of the disks are at a fixed distance D from origin (0, 0), where D > R. It is guaranteed that all the disks lie entirely inside the square.
Suppose, there is a light source at the origin. Find the area of the region of the square that will be lit by this light source. A point inside the square will be lit if the line segment between the origin and the point don’t intersect or touch any of the discs.
SOLUTION
The problem can be solved by doing a radial sweep along the “ring” of discs. Here, we use the fact that the centers of all discs are equidistant from the origin.
We first sort the circles around the center w.r.t. polar angle (the angle made with x-axis) in anti-clockwise order.
For each circle, check if the next circle or previous circle (in the order after sorting) intersect with it or not.
If yes, then the lighted area will be of a shape of a wedge at the center O. Let this wedge be OAB (then AB will part of a sector of the current circle). The points A, B can be finding intersections of the current circles with previous and next circles respectively.
If not, then let us say that next circle doesn’t intersect with the current circle. Then the space lighted between the current circle and the next circle will be a quadrilateral. The coordinates of this quadrilateral can be found by finding the intersection of line segments with the sides of the square.
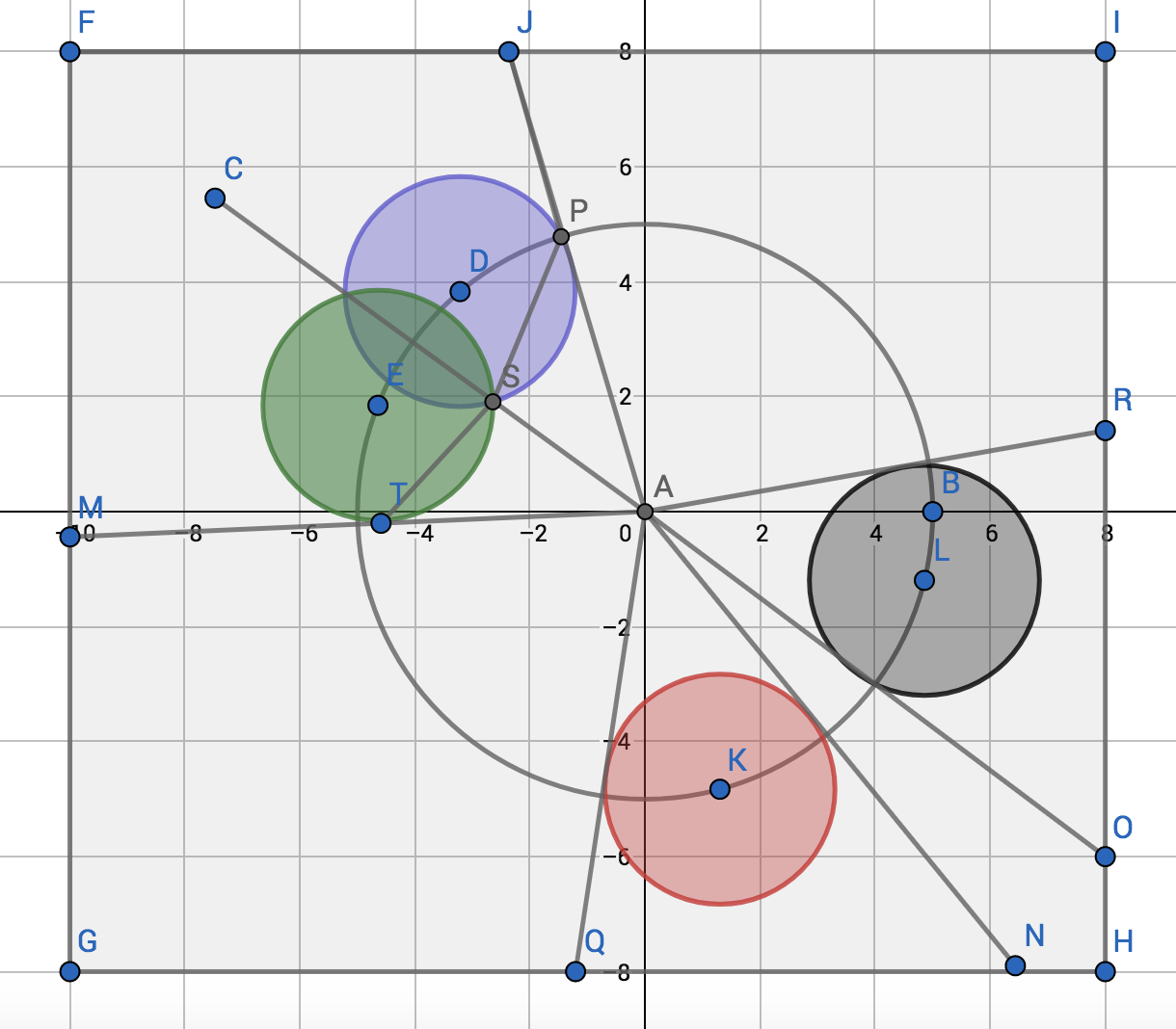
Formally,
For every two adjacent circles c_1 and c_2 (in the sorted order) do -
- If they intersect, draw a ray from origin to point of intersection
- If they don’t draw two rays which which are tangent to the circles c_1 and c_2 respectively. The tangent on c_1 will be the one which is radially closer to c_2. And similarly for c_2.
Now the plane is divided into segments about the origin. Each segment is two rays from origin and either blocked by a circle / quadrilateral / triangle.
You need to compute the area of those segments and add up to give the final answer.
Note that there will be some corner cases in its implementation. Some interesting cases to handle are when there is only one circle. The case where the two consecutive circles only touch each other.
Time Complexity
The time complexity for sorting is \mathcal{O}(N \log N + N * c). Here O© is a significant constant due to calculations involving sin/cos/atan, etc.
Setters and Tester Solution Codes
Setter’s solution
Tester’s solution
Triveni’s solution (follows the approach mentioned in the editorial)
