PROBLEM LINK:
Authors: Jaub Safin
Testers: Vasya Antoniuk
Translators: Vasya Antoniuk (Russian), Team VNOI (Vietnamese) and Hu Zecong (Mandarin)
Editorialist: Praveen Dhinwa
DIFFICULTY:
Medium
PREREQUISITES:
geometry, convex hull, rotating callipers technique
PROBLEM:
You are given N points in 2-D plane. All of the points are distinct. No three of them are collinear.
A polygon is called a 1-concave if it is a simple polygon (its sides don’t intersect or touch) which has at least 1 concave interior angle.
Let S denote the maximum area of a 1-concave polygon with its vertices being choosen from the given N points. You have to output 2 * S.
If it is not possible to construct a 1-concave polygon, output -1.
QUICK EXPLANATION:
If all N points lie on the convex hull, then output -1.
Otherwise construct convex hull of all the points. Also compute an inner convex hull of all points lying inside the just constructed convex hull (outer convex hull).
We can reduce the problem to find the minimum area triangle with two of its vertices belonging to the side of outer convex polygon and the other vertex lying inside the outer convex polygon (to be precise, on the inner convex hull).
We iterate over side of outer convex hull one by one in clockwise direction and consider the side to be the base of the triangle and want to minimize height by taking the third point on the inner hull. Note that third point which has minimum value of height for a fixed side rotates clockwise when we move the side in clockwise direction.
The above observation allows us to apply a two pointer method (or famously called rotating callipers method) to solve the problem in \mathcal{O} (N \, log N) time.
EXPLANATION:
If the constraint of desired polygon being 1-concave polygon is not there, then the maximum area polygon will be the convex hull of all the points.
If all N points lie on the convex hull, then it is not possible to construct a 1-concave polygon.
Now, let us think how we can use convex hull of the points to construct a 1-concave polygon.
Let us think in the reverse way. What minimum amount of area can we lose from the convex hull for getting at least one concave angle.
We can note that if the desired polygon has more than one concave angle, we are going to lose more area. So, we will have just one concave angle, i.e. we will need to create a triangle with two of its vertices lying on the convex hull and other among the points lying inside the convex hull.
Now we can note that if the two vertices on the convex hull are not the adjacent one (i.e. they don’t form a side of convex hull), then we are going to lose more area.
So, now our problem reduces to find the minimum area triangle with two of its vertices belonging to the side of convex polygon and the other vertex lying inside the convex polygon.
A direct implementation of this idea can be done in \mathcal{O}(N^2) time by iterating over each side of the polygon and by trying all the inside points to be a candidate third point of the triangle.
This won’t pass for N = 10^5, we need to make more observations to improve our algorithm.
Let us construct convex hull of the inner points (the points inside the convex hull of all points). From now on, we will distinguish between the two convex hulls by calling them outer and inner convex hulls. We can note that third point of the triangle, which will give minimum area for a side will always lie on inner convex hull.
This can be proved intuitively as follows. Think the side of the outer convex hull as a base of the triangle and we want to minimize the height by picking the third point. Imagine sweeping a line parallel to the side towards the inner convex hull, you can notice that it can never hit a point lying strictly inside the inner convex hull without hitting some point on the inner convex hull first.
Now, we make the final and most crucial observation. When we move along the sides of outer convex hull in clockwise direction, the third point of the triangle also moves clockwise. This observation can be used to have a solution using two pointer method in which first pointer denotes iterates over sides of outer convex hull and the second pointer over the third point on inner convex hull. As we know when we increase first pointer, the second pointer can only increase. Also second pointer can move along the inner convex at most once. So, it will take at max \mathcal{O}(N) iterations.
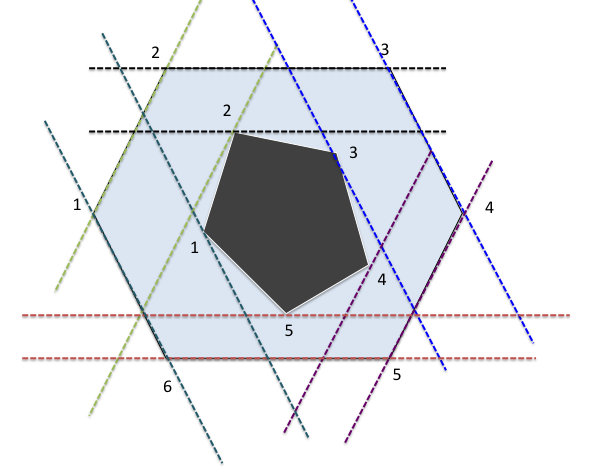
In the above picture,
| Side | Third point |
|--------|-------------|
| (1, 2) | 2 |
| (2, 3) | 2 |
| (3, 4) | 3 |
| (4, 5) | 4 |
| (5, 6) | 5 |
| (6, 1) | 1 |
So, we can notice that when we move along the side in clockwise order, the third point also moves along clockwise order.
long long minTriangleArea = (long long) 1e18;
int second_pointer = 0;
for(int first_pointer = 0; first_pointer < outerHull.size(); first_pointer++) {
long long curArea = abs(triangle_area(outer[first_pointer],
outerHull[(first_pointer+1) % outerHull.size()], outerHull[second_pointer]));
while (true) {
long long newArea = abs(triangle_area(outerHull[first_pointer],
outerHull[(first_pointer+1) % outerHull.size()],
innerHull[(second_pointer+1) % innerHull.size()]));
if (newArea < curr) {
curArea = newArea;
second_pointer = (second_pointer+1) % innerHull.size();
}
else {
break;
}
}
minTriangleArea = min(minTriangleArea, curArea);
}
You can note that we will never have to deal with floating point calculations as the final desired answer is 2 * S.
Time Complexity:
We need to build outer and inner convex hull. Building a convex of N points can be done in \mathcal{O}(N \, log N) time. The two pointer method stated above takes \mathcal{O}(N) time.
So time complexity of the program will be \mathcal{O}(N \, log N) time, which will easily fit in time for N = 10^5.