PROBLEM LINK:
Author: Kaushik Iska
Tester: Jingbo Shang
Editorialist: Ajay K. Verma
DIFFICULTY:
EASY-MEDIUM
PREREQUISITES:
Vertex cover, König’s theorem, Hopcroft–Karp algorithm
PROBLEM:
Given a set of points S in a rectangular grid, find the size of the smallest set T containing rows and columns such that for each point in S either its row or column is in the selected set T.
QUICK EXPLANATION:
The problem can be reduced to finding the size of the optimum vertex cover in a bipartite graph, which can then be computed using Hopcroft-Karp algorithm.
EXPLANATION:
We are given a set of points S, where the demons stand in the beginning. In a single attack Goku can kill all demons in a single row or in a single column.
Since Goku wants to kill all demons, for each demon he must call an attack either on its row or on its column. Hence, the problem is equivalent to find a set T of smallest size containing rows and columns, such that for each demon standing on the point (Rx, Cy) either Rx is in the set T, or Cy is in the set T.
Reduction into vertex cover:
The problem can be easily reduced to finding the optimum vertex cover in a bipartite graph. Let us create a bipartite graph G = (R, C, E), where the vertices on the left side R correspond to rows of the grid, and the vertices on the right side C correspond to the columns of the grid. For each demon standing at point (Rx, Cy) create an edge between the vertex Rx and Cy.
For example, if we have 4 demons standing at (1, 8), (5, 6), (3, 8), (5, 4), we will end with the following bipartite graph:
R = {1, 3, 5}
C = {4, 6, 8}
E = {(1, 8), (5, 6), (3, 8), (5, 4)}
Here each demon is represented by an edge, and in order to kill that demon Goku must pick at least one of its two incident vertices, and call an attack on the picked row (or column), e.g., in order to kill the demon standing at (5, 6) he must attack either Row 5, or Column 6.
In other words, we want to find a set T of smallest size of vertices in the created bipartite graph such that for each edge, one of its incident vertices is in T. Such a set is called vertex cover of the graph.
Finding the Vertex cover:
Finding the optimum vertex cover in a general graph is an NP-hard problem. However, for a bipartite graph the problem can be solved in polynomial time thanks to König’s theorem which states that the size of the vertex cover in a bipartite graph is the same as the size of the maximum matching.
Finding the maximum matching in a bipartite graph is a well known problem, and can be solved in O (E√N) time using Hopcroft–Karp algorithm, where N is the number of vertices and E is the number of edges.
In our problem the number of edges is the same as the number of demons (N). The number of vertices can be at most 2N (N rows and N columns), as each edge will create at most two new vertices.
Use of hash map to create the graph:
In the problem each of the Rx and Cy can be as large as 109. However, there are at most N such values. Hence, one can assign a unique id in [1, N] to each Rx and Cy. A hash map can be used to ensure that the same values of Rx (and Cy) are assigned the same id.
Time Complexity:
O (N1.5)
Weak test cases:
Unfortunately, the test cases for this problem were weak, and allowed greedy solutions to pass. This was pointed out by many participants during the contest. We added new test cases to avoid the false positives, but still there were many solutions which are using greedy and randomized algorithm and are being accepted.
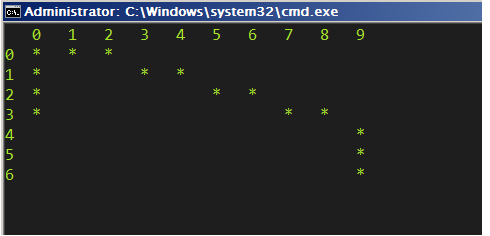
Here is one test case which helped us removing many false positives
1
15
0 0
0 1
0 2
1 0
1 3
1 4
2 0
2 5
2 6
3 0
3 7
3 8
4 9
5 9
6 9
The correct answer is 5, however many accepted solutions were providing 6 as answer.
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution will be put up soon.
Tester’s solution can be found here.