PROBLEM LINKS:
DIFFICULTY
Medium
PREREQUISITES:
Vectors, Convex Polygons, Polyline
QUICK EXPLANATION:
Since we can reuse the vectors and co-line vectors are allowed, it is clear to see that K>=4 for our answer. This is because for K=3, the triangle formed using b[1], b[2] and b[3] can be replaced by a hexagon (b[1], b[1], b[2], b[2], b[3], b[3]) where b[i] represents the ith side. Hence we know 4<=K<=6. We calculate the areas of all polylines of size 2 and 3. Once we have these polylines, for every polyline, we choose a corresponding polyline which can form a closed polygon when the end points of both are joined. We can perform that check by calculating the sum of vectors in both the polylines. If S1 = -S2, then they can form a closed polygon. For details, refer to the detailed explanation. Now for every polyline with sum S, we try to find polylines with sum -S. If we store the polylines in a sorted order(by their sum), we can find the corresponding polylines in log(M) time where M is the number of polylines possible. Also, we only need the maximum area of the polylines for every S. So we only store those values. And we know that every non-convex polygon can be transformed into a convex polygon just by rearranging the order of vectors and the area of convex polygon > area of the corresponding non-convex polygon. Thus, the answer can be found out in O(M log(M)) where M ~ O(N^3).
DETAILED EXPLANATION:
First of all let’s look at the formula for an N-sided polygon having its n-vectors as (x1,y1), (x2, y2) … , (xn, yn) :
Area = 1/2( x1y2 + x2y3 + … +
xny1 - x2y1 - xy2 - … - x1yn)
= 1/2 ( det(1,2) + det(2,3) + … + det(n, 1) )
where det(i,j) = xi.yj - xj.yi
We know that a polar angle of a vector is the counterclockwise angle angle that it makes with the x - axis. Look at the figure for example.
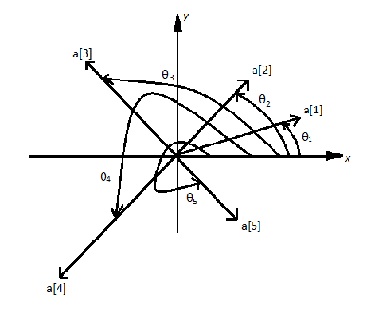
We have N given vectors. Let’s sort them according to their respective polar angles. If the polar angles are same for two vectors, you can choose any order for them. In the above figure, clearly, ?1 < ?2 < … < ?5. Hence the ordering of vectors will be a[1], a[2], a[3], a[4] and a[5].
Now let’s consider a convex polygon with K<=6 vectors. Let us denote it’s sides using b[1], b[2], ... , b[K]. Now, since the polygon is convex, we will have b[1], b[2], ... , b[K] sorted in ascending order of polar angles. This means that if b[1]=a[i[1]], b[2]=a[i[2]]... b[K]=a[i[K]], then i[1] <= i[2] <= .... <= i[K]. Look at the figure for more clarity. We used the vectors from the first figure to form the polygon:
From the polygon formed, consider two polylines with sides b[1], ..., b[K/2] and with sides b[(K+1)/2], ..., b[K]. They are both convex, composed of at most three vectors from our set and what is more important the sequences of indexes of side vectors of these polylines in original sequence a[1], a[2], ..., a[N] are both non-decreasing: (i[1], ..., i[K/2]) and (i[(K+1)/2], ..., i[K]). Also since b[1], ..., b[K] are sides of a polygon which is a closed polyline then b[1]+...+b[K] = 0. And hence
S =
b[1]+...+b[K/2]= -(b[(K+1)/2]+...+b[K])
So polygon (b[1], ..., b[K]) is the union of convex polygons (b[1],...,b[K/2],-S) and (S,b[(K+1)/2],...,b[K]) and hence
area(
b[1], ..., b[K]) = area(b[1], ..., b[K/2], -S) +
area(S, b[(K+1)/2], ..., b[K]).
This idea is clear from the following figure:
We have the basic concepts described now. Let’s move on to the next step. It is easy to see that our answer will always have K>=4. Suppose you have K=3. Then, the triangle formed using b[1] , b[2] and b[3] can be replaced by a hexagon (b[1], b[1], b[2], b[2], b[3], b[3]). This is possible because we can use the same vectors again and co-line vectors are allowed in the polygon. Hence, for any K=3, we always have a larger area with a corresponding hexagon(K=6). Hence, we can now say that **
**. This means that the two polylines of this polygon will have 2 or 3 sides. This simple observation brings us to the following solution:
Take all possible pairs of vectors (a[i], a[j]). This will be a set of polylines with 2 sides.
Take all possible triplets of vectors (a[i], a[j], a[k]). This will be a set of polylines with 3 sides.
Once we have these 2 sets, we can proceed easily towards the solution. We need to combine two polylines such that their end points coincide. For this it is enough to check that the sum of vectors in first polyline = - sum of vectors in second polyline. In other words, if we have a polyline with the sum of it’s vectors = S, we only need to consider those polylines which have their sum = -S. This idea is pretty clear from the previous figure. There it is possible to combine both the polylines.
It’s clear that we only need to store the area and sum of the vectors for any polyline.
Area of a polyline of size 2 i.e. (a[i], a[j]), can be calculated as 0.5*det(a[i] , a[j]) mentioned above. And sum = a[i] + a[j].
Similarly aread of polyline 3 can be calculated as 0.5* (det(a[i], a[j]) + det(a[j],a[k]) + det(a[k], a[i]). And sum = a[i] + a[j] + a[k].
Now that we have both the area and sum for every polyline, we can think of storing them in such a way that our search can be done efficiently. Recall that for every polyline, we need to find the corresponding polyline on the basis of the sum of the polyline. So our search can be optimized if we sort all the polylines according to their sum. Then the search for a particular S can be easily performed in log(M) time where M is the total number of polylines.
Also, we need to maximize the area as much as possible. It is obvious that there can be multiple polylines having the same sum. But, to maximize the area of the polygon formed, we need to consider the polyline with the maximum area. So, for every S we calculated, we only need to store the polyline corresponding to the maximum area. For all such polygons which can be formed, we calculate the area as the sum of its two corresponding polylines and our final answer will be the maximum out of these calculated areas. Also we need not worry if the polygon formed is convex or not. This is because, if we have a non-convex polygon, there will always be a corresponding convex polygon that can be formed by modifying the order of the vectors. This idea is demonstrated by the following figure:
Clearly, the area of the corresponding convex polygon will always be larger than the non-convex polygon.
Thus, we have our answer in O(M*log M) time complexity.
SETTER’S SOLUTION
Can be found here.
APPROACH
The problem setter used the above approach to solve the problem.
TESTER’S SOLUTION
Can be found here.
APPROACH
The problem tester used the above approach to solve the problem.
