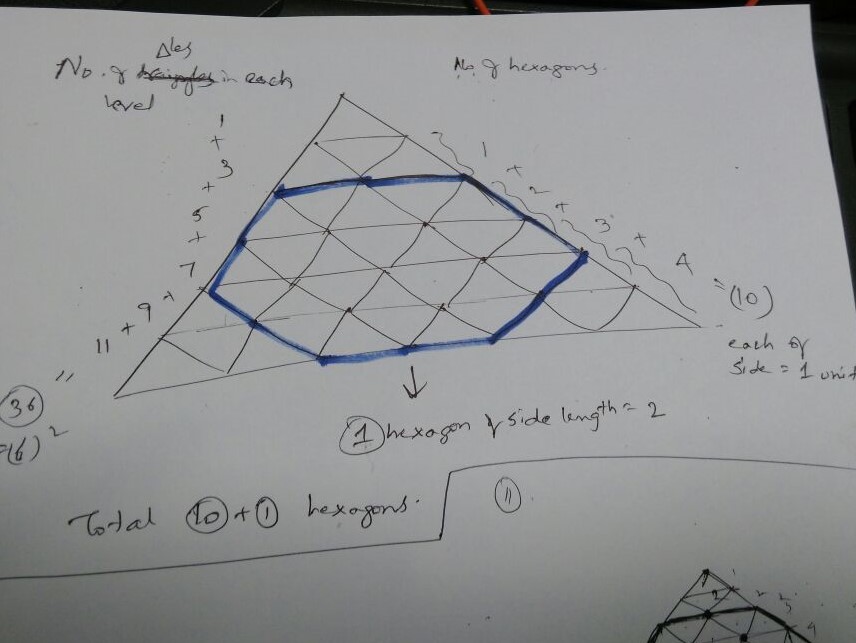
http://math.stackexchange.com/questions/2214496/project-euler-577-confusion this link will be helpful I guess.I drew it manually and you need to consider sqrt(3) also has one of the side, see second image.
So, according to me number of hexagons will be equal to number of hexagons with side of length one which is equal sum of integers from 1 to n-2 plus number of hexagons with side of length two and so on. May be this much could help you to further figure out the formula.
I gave my best, even I am trying to figure out the formula. Let me know if you get it. Thank you.
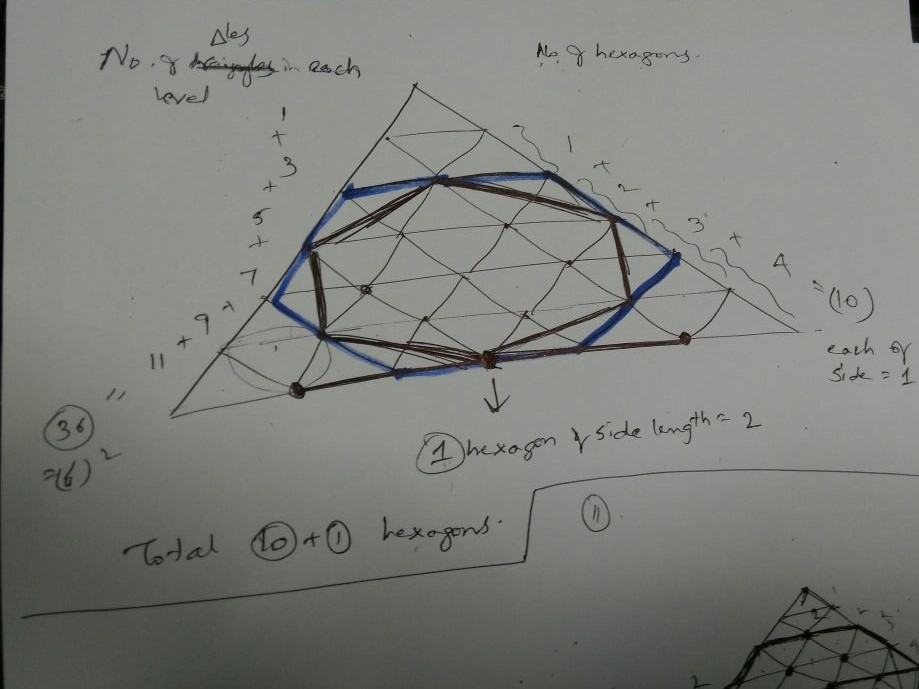
I managed to find the other hexagon:- (with black bold lines in the diagram)
i also used same approach but how H(20)=966
n max side of hexagon
3 1 unit [(n-2)+(n-3)+(n-4)…1]
6 2 unit 2[(n-5)+(n-6)+…1]
9 3 unit [(n-8)+(n-9)+…1]
12 4 unit 2[(n-11)+(n-12)+…1]
so if n=12 then formula may be
[(n-2)+(n-3)+(n-4)…1]+2[(n-5)+(n-6)+…1]+[(n-8)+(n-9)+…1]+2[(n-11)+(n-12)+…1]
so am i right or not