PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Setter: Praveen Dhinwa
Tester: Teja Vardhan Reddy
Editorialist: Taranpreet Singh
DIFFICULTY:
Medium-Hard
PREREQUISITES:
Observations, Max Flow and Matching algorithms in Bipartite graphs and Kőnig’s theorem. Understanding of Segment Tree is also required.
PROBLEM:
Given a pond of dimension N*N with N elephants standing at each side just outside pond, having their trunks expanded in the straight line without colliding with the trunk of the elephant standing at opposite side, Find out the minimum number of elephants to be removed in order to ensure that no elephant’s trunk collide.
Further given that Trunk lengths for any side are in increasing or decreasing order only.
QUICK EXPLANATION
- Building graph with elephants as vertices and edges between pairs of elephants whose trunks collide. We can see, that we have a Bipartite graph.
- Required answer is actually the maximum flow in a graph where vertices of one set are connected to the source while vertices present in the Second set are connected to sink, all edges having a unit capacity.
- Naively doing so will lead to TLE, so, we will Build a Segment tree type flow network for that set of vertices connected to sink to reduce the number of edges. added to the graph. This work because trunk lengths of elephants are in increasing/decreasing order, assuring that one vertex of the first set will be connected to a range of consecutive vertices of the second set, for each side only.
EXPLANATION
Let us consider Each elephant as a graph vertex and add edges between two vertices if the trunk of corresponding two elephants collides. Checking this can be referred in secret box below.
Click to view
An elephant in row x can meet an elephant in column y at position (x, y) only. So, just check, if trunks of both elephants reach position (x, y) or not.
Lemma: Minimum number of vertices we need to remove to remove all edges is the Minimum number of elephants to remove.
Reason: We see, that each edge represent an intersection of trunks of a pair of elephants. We need no intersection while removing the minimum number of elephants, so, Removing the minimum number of vertices to remove all edges is sufficient.
Now, Considering the property that No two opposite elephant’s trunks can collide, we can divide vertices into two sets, one set containing elephants at North and South direction while other set containing elephants at east and west direction.
We know that Opposite elephants trunks do not collide, hence, there will be no edge with both end points in the same set, so we always have edges having one end in one set and opposite end in the second set. These type of graphs are also known as Bipartite Graphs.
So now, Our problem becomes to calculate Minimum Vertex Cover in the bipartite graph.
To calculate this, Kőnig’s theorem come to rescue, which states that the Minimum Vertex cover of a bipartite graph is the same as the maximal matching in a bipartite graph.
Finding the maximal matching can be done using Max Flow algorithms.
But the Number of edges in this approach is too much, leading to TLE verdict.
So, To Reduce Number of edges, we shall use the last property about trunk lengths mentioned in constraints, that lengths of trunks are always in increasing/decreasing order for all sides. Using this, It is not hard to see that Each vertex shall be incident to a consecutive range of vertices on a side.
Using this, let us organize the vertices in the second set in a special fashion, which uses a lesser number of edges, in Segment tree style. 
If we remember segment tree correctly, we can see, that root consisted of whole range [1, N], and as we moved downward, the range of vertices reduces till it gets reduces to 1.
Click to view
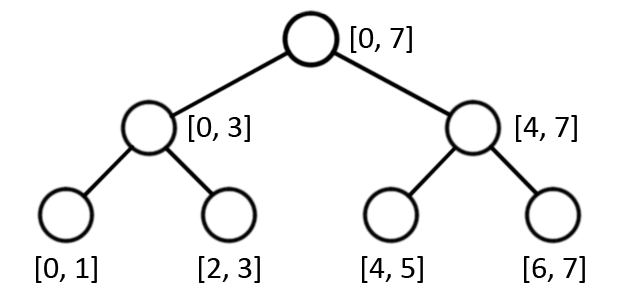
Suppose we have built the network, with all elements of the first set being connected to the source with edges having a unit capacity as well as vertices of the second set connected to sink with edges of unit capacity. Now, Let us make internal nodes, representing a range of nodes, with edge capacity being the number of vertices in the range of the child. The root of Segment Tree shall consist of whole range [1, N].
The important property of segment tree that makes it useful for us today is, that we can represent any range [L, R] having 1 \leq L \leq R \leq N using at most logN nodes of segment tree. This allows us to connect any vertex of the first set with a range of vertices in the second set by connecting that vertices to at most logN nodes only, leading to Number of edges being bounded by a multiple of N*logN, which is much better than N*N edges in naive solution.
Since we have two sides in the second set, there will be two segment tree structures for efficiently adding edges. We can find the ranges naively too since Constraints allow N^2 pass over the combination of Row and Columns.
Hence, The final solution looks like: we can build the segment tree structures for both present in sides in the second set, Find ranges of vertices in the second set with which any vertex of the first set collides. Connect That vertex with all vertices in range using at most logN additional edges and finally print the maximum flow in this Flow Network.
Related Problem can be found here.
Time Complexity
Initially, the pass over all combinations of row and column to calculate ranges take O(N^2) time. Number of vertices in graph build are precisely 2+2*n+2*2^{\lceil log_2 N\rceil}. The number of edges added in segment tree is of order N*logN for each tree while Number of Edges added due to intersections is also N*logN, leading to Number of edges being a multiple of N*logN.
So, Assuming Dinic’s Max flow algorithm is used, It is not hard to notice that there will be exactly logN phases leading to O(V*E*logN) time. Since we have V of order N and E of order N*logN, we get overall Time complexity O(N^2*log^2N).
Proof of Number of vertices and edges in this Flow Network is left as an exercise.
AUTHOR’S AND TESTER’S SOLUTIONS:
Setter’s solution
Tester’s solution
Editorialist’s solution
Feel free to Share your approach, If it differs. Suggestions are always welcomed. 

