DEVLDISC - Editorial

editorial
, , , ,
1

PROBLEM LINK:

Practice
Contest

Author: Praveen Dhinwa
Tester: Istvan Nagy
Editorialist: Miguel Oliveira

DIFFICULTY:

Simple

PREREQUISITES:

Graph Theory

PROBLEM:

Given a positive integer N up to 50, find if the following algorithm computes the longest shortest path in any connected undirected graph with N vertices. If it doesn’t, output any graph in which this algorithm doesn’t work correctly.

Algorithm (start_vertex):
	find out the set of vertices S having maximum value of 
		shortest distance from start_vertex.
	ans = 0;
	for each vertex v in S
		temp = 0;
		for each vertex u in graph G:
			temp = max(temp, shortest distance between u and v).
		ans = max(ans, temp);
	return ans;

EXPLANATION:

The given algorithm works if the given graph was a tree (explanation). However, as the problem statement suggests, it does not always work in a general graph.

This problem is unusual. Instead of finding an algorithm to solve a problem, we need to find out why the given algorithm is incorrect. So, pen and paper are best to tackle this challenge!

Without loss of generality, I will assume for simplicity that there is only one vertex S furthest away from start_vertex. For the algorithm to be flawed, S can not be one the two end-points of the longest shortest path. Also, S must be closer to all vertices than the length of the longest shortest path.

The simplest way to do this is to use a longest shortest path of length 4, put S at distance 3 away from start_vertex and all other vertices at distances 1 or 2 from start_vertex.

Suppose the longest shortest path is a path like 1 - 2 - 3 - 4 - 5 (length 4). To have start_vertex at distance up to 2 to all of them, adding edges (start_vertex, 2), and (start_vertex, 4) is sufficient.

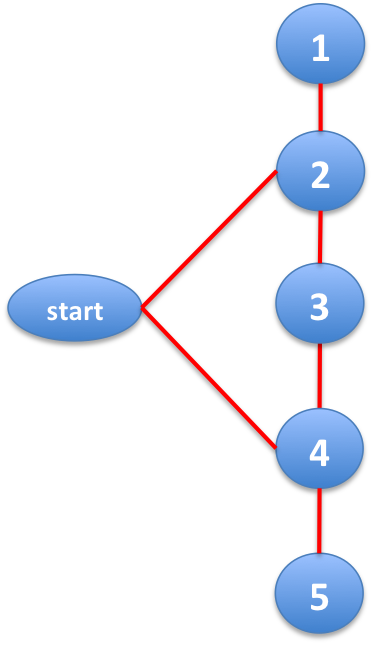
disc1

Now, we want to have S at distance 3 from start_vertex and distance at most 3 from the others so that we can’t find a path of length 4 from S. So we connect S to vertex 3.

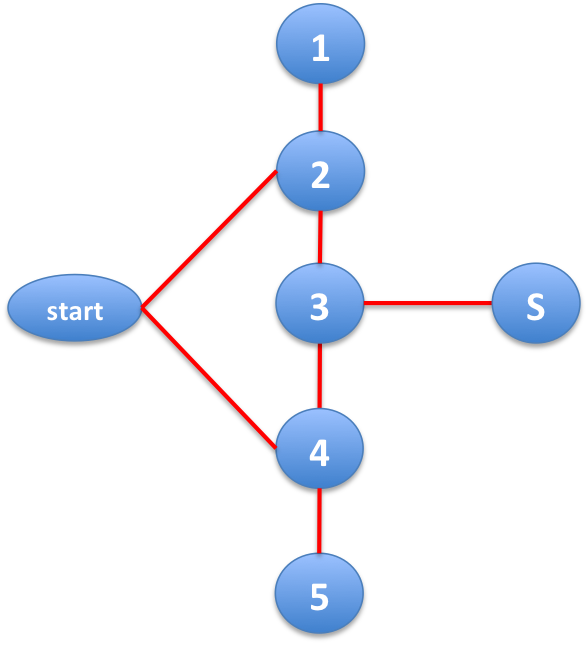
disc2

Finally, we can connect all the other vertices to either vertices 2 or 4. This way, all of them are at distance 2 from start_vertex and distance 3 from S. Hence, the algorithm will only find paths of length up to 3.

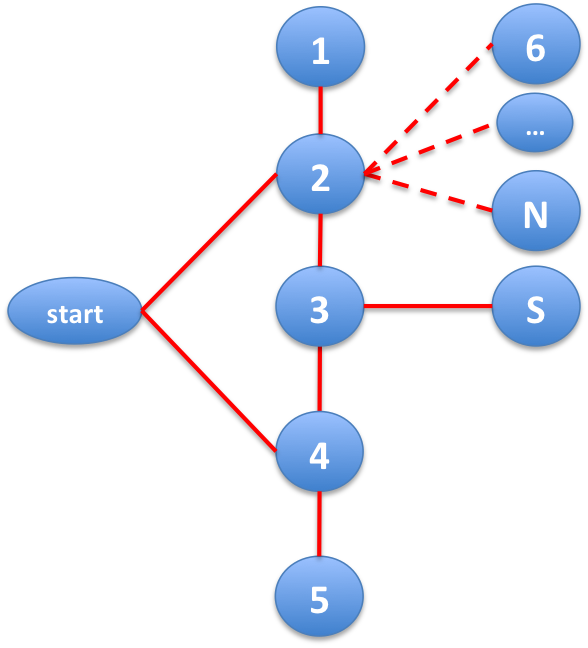
alt text

To be able to use this construction, we need at least 7 vertices. So, there is always a counter-example if N \ge 7. We can check by brute force that it’s impossible to do this if N \leq 6.

For each input, we only need N edges, so the time complexity of this approach is O(N) per test case.

Sample Solutions

Author
Tester

2

Please check my solution . I did the same and could not get AC .

3

@osho1278

for n>7 you should add two new edges between node 3 and 6 and you added them between 2 and 4 , so it showed WA

4

@osho1278

Your basic graph of 7 vertices is correct. But you are making a mistake in adding the extra vertices.
You start adding the extra edges to vertex 2 with the vertex 7 instead of 8. This makes the longest shortest path 3-2-7 instead of 3-2-6-7. Change your loop to i=1 to n-7 instead of i=0 to n-6.

5

I used a randomly written random connected graph generator and for each graph I used Floyd-Warshall to implement the algorithm as described in the problem. Turns out I can generate a counterexample graph for n = 7 to 50 in ~1s.

1 Like
6

Another solution-

for n>=8 Make two triangles . Join them base to base via two edges .Two triangles will cover 6 verices. Remaining vertices(RV)=n-6;

Now divide these remaining vertices into 2 parts 1st part contains (RV1) =RV/2(vertices) , 2nd part contains (RV2) =RV-RV1 (vertices)

Now fit these RV1 vertices on either of the edge that joins base vertices and fit RV2 vertices on other edge joining base verices of two triangles.

Consider the shortest distance between extreme ends of two triangles(non-base vertices) as the longest path and number all vertices accordingly.

1 Like
7

solution

This was my pen and paper approach for graphs with 7,8,9 vertices and then a general graph for >=10 vertices :slight_smile:

8

My starting point is always node ‘1’. For N<7 it will be always ‘-1’. So, for N>=7

For N%2==0

A cycle using nodes 1,2,…,N-2 where (1) and (N-2) are directly connected and have attached (N-1) -> (N-2) and (N) -> (2)

1->2

2->3

3->4

.

.

.

(N-2)->1

(N-1)->(N-2)

N->2

For N%2==1

A cycle using nodes 1,2,…,N-1 where (1) and (N-1) are directly connected and have attached (N) -> (N-1)

1->2

2->3

3->4

.

.

.

(N-1)->1

N->(N-1)

9

My Solution :

Initially actually wrote a program to brute force all permutations of a graph and check for a counter example with every start vertex. Thankfully I found a solution for n=7 and from there on i just had to find a pattern :slight_smile:

Let me know if this was your graph too :slight_smile:

#(start vertex can be 1 or 5 in the below graphs)
Graph 1

Graph 2

2 Likes
10

My Approach :
If N is even : create a ring of size N-2
else create a ring of size of N-1
for example if N=8

1–2--3

|…|

6–5--4

attach the remaining nodes to node 6 and start from 1.

Implementation

1 Like
11

Can someone please tell me how my solution is incorrect? Start vertex is 1.

For a graph having odd number of vertices, I make a circle of size N - 1, and attach the Nth node to 2:

1–> 2

2 --> 3

3 --> …

N-1 --> 1

N --> 2

For a graph having even number of vertices:

Again, a circle with N - 1 nodes and Nth node attached to 2. But the 1st node is now also attached to the N-2 node.

The longest path in each case is from node N-1 to node (N - 1)/2

https://www.codechef.com/viewsolution/9356098

12

Look like we both had the same logic :slight_smile: Later I figured out that you can keep the ring size to a constant 6 and attach the rest to node 6 and then start at 1 :slight_smile:

13

This is interesting. It did not occur to me that probably of finding these kinds of graph seems to be quite high.

14

LInk to practice prob is pointing towards STROPR problem and Sample solution links points to the editorial page itself. Need to be fixed soon !!!

15

Thanks, I fixed the practice problem link. I already notified the Codechef team about the solutions links.

16

Thanks @mogers

17

Can anyone explain why we can’t have our solution for n<=6 ?

18

Why can’t we have solution for N<=6 ? Can you please explain this in detail ?