Tree
A tree is a non linear data structure . It is a finite collection of nodes that reflects one to many relationship. It is hierarchical structure.
The connection line between two nodes is called edge.
The topmost node is called root of the tree.
The element that are directly under an element are called its children.
The element directly above something is called its parent.
Except the root each element has a parent.
The node that has child node is called parent node.
Two nodes that have the same parent are called sibling.**
A node that is connected to all lower-level nodes is called an ancestor.
The connected lower-level nodes are descendants of the ancestor node.
Height of a node is the number of edges between the target node and furthest leaf node.
Depth of a node is the number of edges between the target node and root node.
Applications of tree:
1. File system.
2. Storing hierarchies in organizations
3. Router algorithms
Binary Tree: A tree whose elements have at most 2 children is called a binary tree.
Mainly Here we discuss about the Binary Search Tree
Binary Search Tree : A Binary Search Tree is a binary tree where all the node value of the left subtree are smaller than or equal to the root node value and the node value of the right subtree are larger than or equal to the root node value.
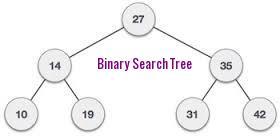
Before doing binary search tree we need to define structure for binary search tree.
struct bst
{
int data;
bst *left;
bst *right;
}*root=NULL:
BST Creation :
Algorithm : creation(data) Step 1: Start Step 2: Set newnode = new bst Step 3: Set newnode.data = data Step 4: Set newnode.left = newnode.right = NULL Step 5: return newnode Step 6: End
bst *creation(int data) { bst *newnode = new bst; newnode->data = data; newnode->left= newnode->right = NULL: return newnode; }
Inorder traversal Algorithm:
Inorder(root) Step 1: Start Step 2: if root!=NULL inorder(root.left); print root.data; inorder(root.right); Step 3: End. C++ implementation: void inorder(bst *root) { if(root!=NULL) { inorder(root->left); cout<<root->data<right); } }
BST Seach Algorithm:
Search(root,data) Step 1: Start Step 2: if (root==NULL) return false; else if(root.data = data) return true else if(root.data < data) return search(root.right, data); else return search(root.left, data); Step 3: End C++ implementation: bool search(bst *root,int data) { if(root==NULL) return root; else if(root->data = data) return true else if(root->data < data) return search(root->right, data); else return search(root->left, data); }
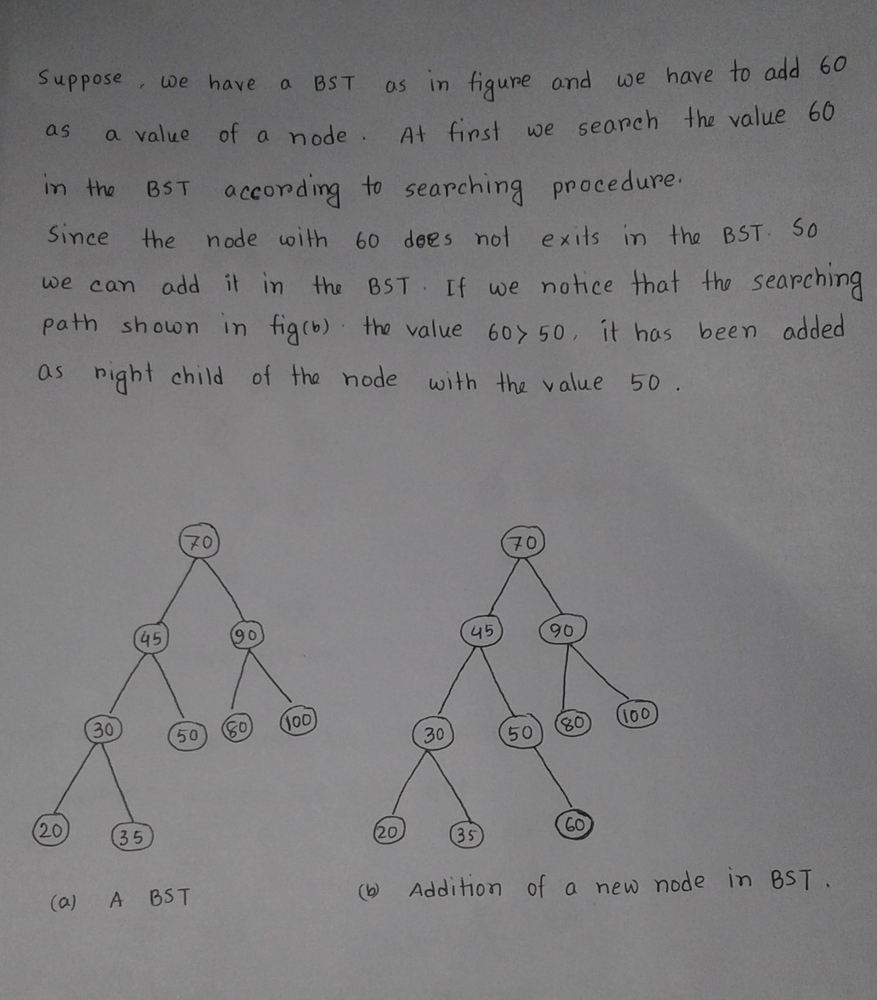
Insertion Algorithm:
Insertion(root,data) Step 1: Start Step 2: if (root==NULL) root = creation(data); else if(root->data < data) root.right = Insetion(root.right, data); else if(root->data > data) root.left = Insertion(root.left, data); else return root; Step 3: End C++ implementation: bst *Insertion(bst *root,int data) { if (root==NULL) root = creation(data); else if(root->data < data) root->right = Insetion(root->right, data); else if(root->data > data) root->left = Insertion(root->left, data); else return root; }
Function to find minimum in a tree.
bst* FindMin(bst* root) { if(root==NULL || root->left ==NULL) return root; else return FindMin(root->left); }
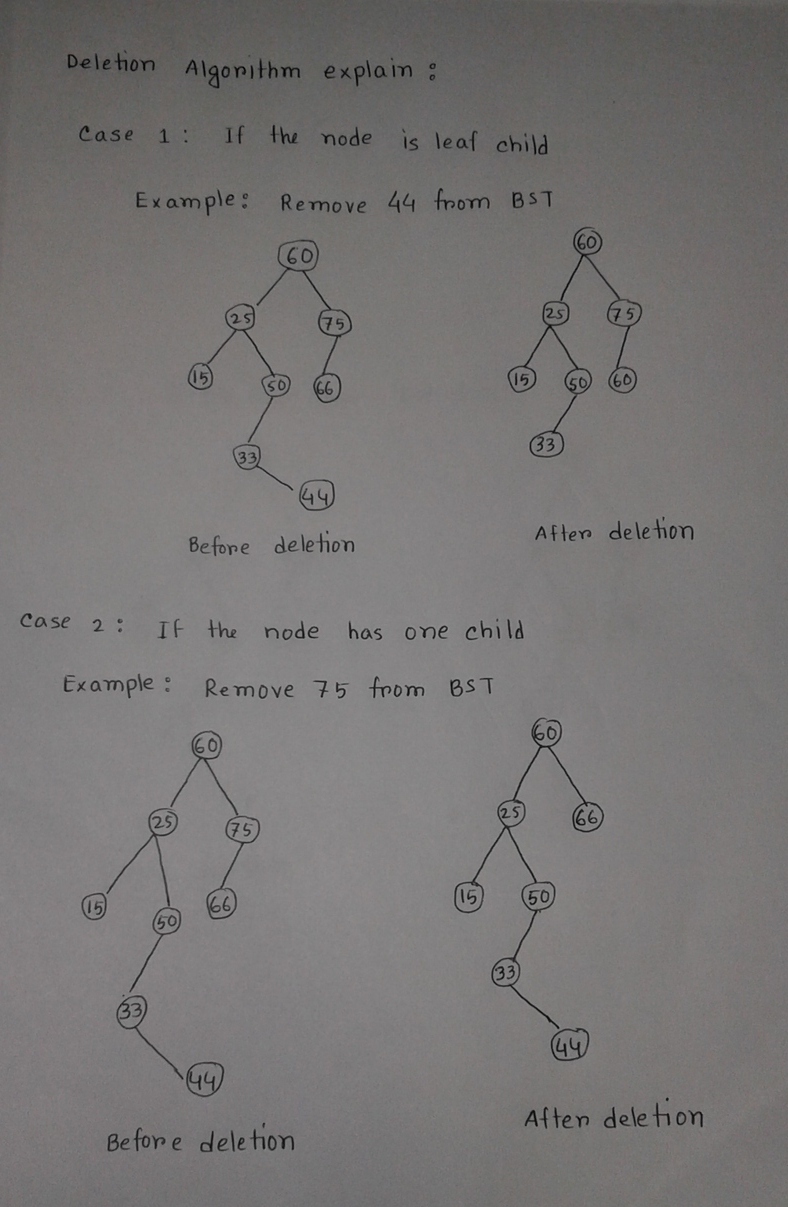
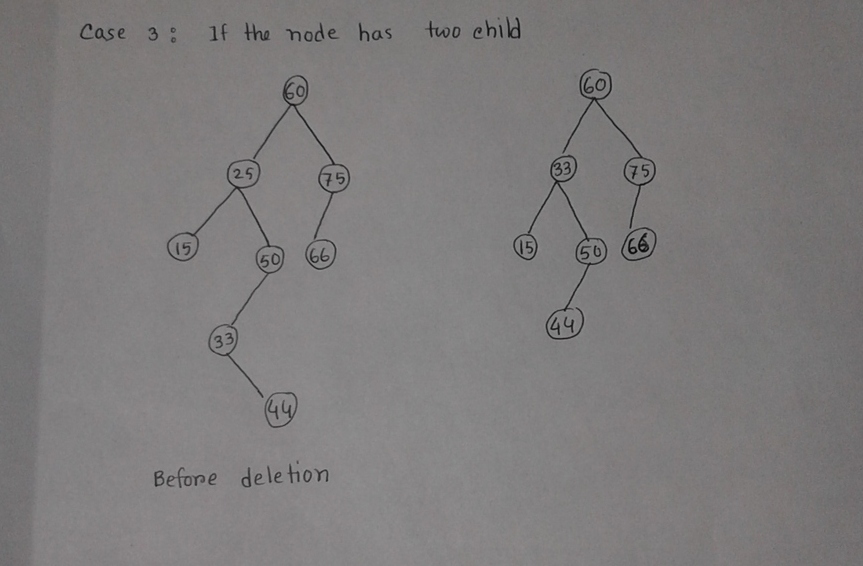
Deletion Algorithm:
Deletion(root, data) Step 1: Start Step 2: Locate the node to be deleted Step 3:Three Case can be considered Case 1 : If the node is leaf node: i.If the node is left child of the parent, make NULL the left pointer of its parent node and free the space for the node. ii.If the node is right child of the parent, make NULL the right pointer of its parent node and free the space for the node. Case 2: If the node has one child: i.If the node to be deleted is left child of its parent, then make link between the left pointer of its parent node and child node(left or right) of the node to be deleted. Then delete the node. II.If the node to be deleted is right child of its parent, then make link between the right pointer of its parent node and child node(left or right) of the node to be deleted. Then delete the node. Case 3: If the node to be deleted has two children: Find the the node with minimum value from the right sub tree (the node to be delete).Replace the node value to be deleted .Delete the target node. Step 4: ENd. C++ implementation : bst *Deletion(bst *root, int data) { if (root==NULL) return root; else if(root->data > data) root->left = Deletion(root->left, data); else if(root->data < data) root->right = Deletion(root->right, data); else { if(root->left==NULL && root->right==NULL) { delete root; root = NULL; } else if(root->left==NULL) { bst *temp = root; root = root->right; delete temp; } else if(root->right==NULL) { bst *temp = root; root = root->left; delete temp; } else { bst *temp = FindMin(root->right); root->data = temp->data; root->right = Deletion(root->right, temp->data); } } }
Height Of BST :
Height Of Binary search tree is the number of edges between the root node and furthest leaf node.
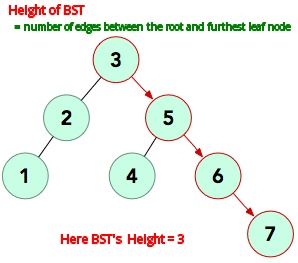
Algorithm : Height(root)
Step 1: Start
Step 2:if (root==NULL) return -1;
else return max(getHeight(root.left), getHeight(root.right)) + 1;
Step 3: End
C++ implementation :
int getHeight(Node* root) {
if(root == NULL) return -1;
else return max(getHeight(root->left), getHeight(root->right)) + 1;
}
if(root == NULL) return -1;
else return max(getHeight(root->left), getHeight(root->right)) + 1;
}
Full Source code : Link
Hackerrank Problem : Binary Search Tree : Insertion, Inorder Traversal, Binary Search Trees, Height of a Tree