CR195 - Editorial

editorial
, , ,
1

Contest
Practice

Author: Shivam Garg

DIFFICULTY

Medium Hard

PREREQUISITES

Matrix Exponentiation, Solving Linear Equations

PROBLEM

Given an integer n, find the number of n length strings comprising only L,R,D,U characters such that i^{th} and i+2^{th} characters are never same, and no substring of length 4 must be of the type URDL, RDLU, DLUR, LURD, ULDR, LDRU, DRUL, and RULD.

EXPLANATION

This question requires knowledge of Matrix Exponentiation. So, I would advise you to go through this tutorial, and solve questions at the end in case you don’t have a basic idea about this topic.

Now, try to form an adjacency matrix M [ ] [ ], where M[i][j] denotes the number of ways to go from a 3 letter state to another 3 letter state.
As there are 4 letters for each position, the initial matrix will be of size 4^3*4^3.

So let’s say you have a three letter state (i, j, k), and you want to go to another three letter state (x, y, z).
For that you can run a nested loop of 64*64, and need to ensure that j==x and k==y, and then ensure the 4 characters than form now (i, j, k, z) should follow all the constraints/conditions that follow.

for(a = 0 ; a != 64 ; a++)
{
    for(b = 0 ; b != 64 ; b++)
    {
	    [i, j, k] = hash [ a ]; //assume some hash to map 3 characters to a value
	    [x, y, z] = hash [ b ];
	    if ( j != x || k != y ) continue;
		if ( i == k || j == z ) continue;  
	    if ( i == 0 and j == 1 and k == 2 and z == 3 ) continue;
	    // Other 7 cases follow....
	    //........
	    M[a][b] = 1;
	 }
}

Now, this 64*64 matrix will lead to O(T*64^3*log\,n), where 1<=n<=10^{18}, and 1<=T<=10^4. This will obviously time out.

For handling this situation, obtain some of the starting 8-9 solutions, namely - 4, 16, 48, 136, 392, 1128, 3240.
Try forming 3-4 linear equations with these solutions of the following form:-

136x_1 + 48x_2 + 16x_3 = 392
392x_1 + 136x_2 + 48x_3 = 1128
1128x_1 + 392x_2 + 136x_3 = 3240
…

Now, if you try to solve them via any method for solving linear equations, let’s say Gauss Elimination, you will find out that we will get -

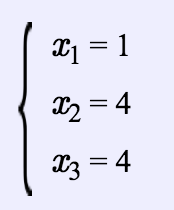
alt text

Thus, now you can form a matrix A [ ] [ ] = \begin{bmatrix} 1 & 4 & 4 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{bmatrix}.

Hence, if you do the matrix exponentiation on this 3*3 matrix, the final answer shall be
136*A(0,0) + 48*A(0,1)+ 16* A(0,2).

This will now reduce the complexity to O(T*3^3*log\,n), which is enough to pass within the given time constraint.

RELATED QUESTIONS

Codereds 2018’s KRYP3
Geekhaven 2017 Contest’s Goku and another problem
Geekhaven 2018 Contest’s The East Wind Is Coming

2 Likes
2

How did you decide answer for Nth number is dependent on N-1 ,N-2 , N-3 terms

1 Like
3

And I also don’t understand why using the equation

48x_1 + 16x_2 + 4x_3 = 136

in place of the last equation doesn’t work. That method yields

x_1 = 2.33333, x_2 = 1.33333, x_3 = 0.666667
4

In any circular/rotating step, you must at any point of time ensure the dependency of previous 3 characters. Let’s say you have URD, now in this case you can’s place L as last 3 characters are against the rules.

This is the reason you need to have dependency on last 3 characters.
Why the very first answer i.e 4 doesn’t contribute to the correct matrix is because it never helps in developing the constraint. It may be confusing, but yeah if one tries to figure out mathematically, one will get that this value never helps in reaching answer 16 under any of the constraint.

5

Whether we can place a character at a particular position or not definitely depends on the last 3 chars but does that necessarily imply that no. of N length strings will be a function of no. of (N-1), (N-2) and (N-3) length strings and more specifically a linear function ? This part is confusing.

2 Likes
6

@roll_no_1 Yeah thats my question how can one get this intuition ?

7

And how did we already know that they linearly depending only? They could be quadractically dependent also.