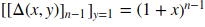PROBLEM LINK:
Contest
Practice
Author:Tapish Pratap Singh
Tester:Arnab Samanta
Editorialist:Tapish Pratap Singh
DIFFICULTY:
Hard
PREREQUISITES:
Math, Combinatorics, Pascal Triangles
EXPLANATION:
The sequence in the question is the generalisation of Moessner sequencce. In Moessner sequence d_1=d_2=........d_{m-1}=d_{m}.
Consider N=8, m=2, d_1=d_2=4
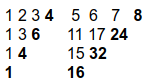
As we can observe every group satisfy the Pascal property (each interior element is the sum of the elements immediately above it and to its left).
Lets add a new row and column of 1’s in the first group.

Pascal Traingle
Similarly for Second group add a new row of 1’s and a column containing previously marked numbers,

Now we will represent the above sequence algebraically using Pascal triangle.
Let h_k(x,y) be the algebraic representation of the kth triangle.
So, h_k(x,1) will be the polynomial having coefficients as the marked numbers for the kth triangle then,
Each triangle is obtained from the previous by taking the homogeneous component of degree diff_k, and multiplying by ∆(x,y) and then putting y=1 in the obtained triangle.
h_{k+1}(x,y)=[h_k(x,1)*∆(x,y)]_{d_k} and h_0(x,1)=1 where d_k is the size of group k and
∆(x,y) =\frac{1}{1-(x+y)}=(x+y)^0+(x+y)^1+(x+y)^2+...=\sum_{d=0}^{\infty}(x+y)^d
(Note:-∆(x,y) is the algebraic representation of pascal triangle.
The nth north-east to south-west row of the pascal triangle will be:-
[[\Delta(x,y)]_{n-1}]_{y=1}=(1+x)^{n-1})
which simplifies to
h_k(x,1) = \prod_{i=0}^{k-1}((k-i)*x+1)^{diff_i}) where diff_i=d_i-d_{i-1} and d_0=0
Now what we require is the sum of all marked numbers in the original group which is:h_k(x,1)-1 (subtracting 1 as we added the rows of 1’s ,so 1 needed to be subtracted)
Final ans:-
\sum_{k=1}^{m}(h_k(x,1)-1)
Eg:-
Consider n=4,m=2,d_1=d_2=2
now h_0(x,1)=1
now
h_1(x,y)=[h_0(x,1)*∆(x,y)]_2=[1*((x+y)^0+(x+y)^1+(x+y)^2+...)]_2=(x+y)^2
h_2(x,y)=[h_1(x,1)*∆(x,y)]_2=[(x^2+2x+1)(1+x+y+x^2+y^2+2xy+...)]_2=4x^2+4xy+y^2
now h_1(x,1)=1+2x+x^2 represents the first modified triangle
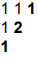
and
h_2(x,1)=1+4x+4x^2 represents the second modified triangle

TIME COMPLEXITY:
O(m*m*log(max(diff[i])))