CIRCLEQ - Editorial

[tsreaper]

PROBLEM LINK:

Practice
Contest

Author: amrmahmoud
Tester: dpraveen
Editorialist: tsreaper

DIFFICULTY:

Medium-Hard

PREREQUISITES:

BIT/Fenwick Tree, Geometry

PROBLEM:

Given N circles. No two circles touch or intersect each other. Given Q queries. Each query is a rectangle. Calculate the total area of the circles within the rectangle.

EXPLANATION:

Let ans(x_1,y_1,x_2,y_2) be the answer of the rectangle whose left-down corner is (x_1,y_1) and right-up corner is (x_2,y_2), it’s obvious that:

ans(x_1,y_1,x_2,y_2)=ans(0,0,x_2,y_2)-ans(0,0,x_1,y_2)-ans(0,0,x_2,y_1)+ans(0,0,x_1,y_1)

So we can divide one query into four queries, now what we need to focus on is the total area of the circles within the rectangle whose left-down corner is (0,0) and whose right-up corner is (x',y').

Let’s define the right-up point of a circle whose center is (x_0,y_0) and whose radius is r as (x_0+r,y_0+r). For each rectangle we need to calculate, there are 3 kinds of circles.

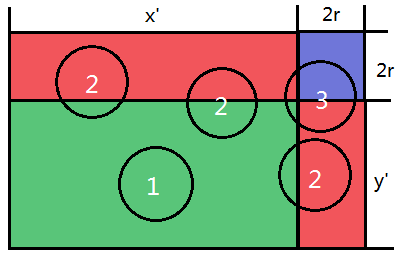
1. The right-up point of the circle is in the green rectangular area, so the whole circle is within the (0,0,x,y) rectangle. To solve this part of the problem, we need to sum up all the areas of the circle whose right-up point is in the green rectangular area. This is a classic two dimensional partial order problem which can be solved using BIT/Fenwick tree.

2. The right-up point of the circle is in the red rectangular area, so the straight line x=x' or y=y' goes through the circle and divide it into two halves. For a circle whose radius is r, there are at most 4r lines which go through the circle. For each line, we can pre-calculate which circles it goes through. Then for each query, we can use binary search to find the right most circle which x=x' goes through and whose right-up point is in the red rectangular area and sum up the areas. We can do the same thing for y=y'.

3. The right-up point of the circle is in the blue rectangular area. Note that no two circles touch or intersect each other, so for a fixed radius r, there are at most 2 circles whose right-up point is in the blue rectangular area. So we can loop through all r, and calculate the areas directly.

Sum all the three kinds of areas up, and we get the answer.

TIME COMPLEXITY:

For the first kind of circle, the time complexity is O((N+Q)logX), where X=50000.

For the second kind of circle, the time complexity is O(NR+XlogX+QlogX), where X=50000 and R=50.

For the third kind of circle, the time complexity is O(QR), where R=50.

MY SOLUTION:

My solution

(Sorry for the poor English.)

[ganeshk2]

Implemented this but when storing the sum of areas in the BIT, i guess the precision decreases very fast for large number of circles.
Got WA for all subtasks when using double, got AC for random subtasks when long double is used for the same code. Didn’t work finally though !

[tsreaper]

You are right. The disadvantage of this solution is its low precision. But I think there may be other problems in your implementation. I got WA only on test 14 and 15 when using double and got AC when using long double.

[darshil_babel]

Can you explain how you reach here:

ans(x1,y1,x2,y2)=ans(0,0,x2,y2)−ans(0,0,x1,y2)−ans(0,0,x2,y1)+ans(0,0,x1,y1)

In problem statement it is written that “find the total area covered by restaurants in the rectangle defined by the points x1, y1, x2, y2 where (x1, y1) is the lower left corner and (x2, y2) is the upper right corner.”

So, if we consider a circle with two diameter end points as (x1, y1) and (x2, y2) then there can be infinitely many rectangles whose total area equals area of circle. So why are we not considering this area here?

[prudvinit]

Hello tsreaper, I would be very greateful if you told me how to find the area enclosed by the circles in green area by using fenwick trees.

[tsreaper]

To prudvinit:

Let’s consider this question.

There are N value points. The coordinate of the i-th point is (x_i,y_i) and its value is v_i. There are Q query points. Each query (X,Y) asks us to calculate the total value of points which satisfy x_i \le X and y_i \le Y.

We can sort all the value and query points together in the increasing order of their x-coordinate. If two points has the same x-coordinate, then sort them in the increasing order of their y-coordinate.

After sorting, the x-coordinate of each point is larger than or equal to the x-coordinate of the points which has a smaller index. Now for each query point, we need to know “the total value of the points which has a smaller index and has a smaller y-coordinate”. This can be done by putting the points into a fenwick tree. The index of the fenwick tree is the y-coordinate of the point, and the value of the fenwick tree is the value of the point.

[tsreaper]

Sorry, I can’t quite understand this question. I think you can consider “how to calculate the sum in a rectangle if I know the prefix sum” and then you may understand.

[prudvinit]

Thanks tsreaper