PROBLEM LINK:
Author: ???
Tester: Kevin Atienza, Jingbo Shang
Editorialist: Kevin Atienza
PREREQUISITES:
Lowest common ancestor, inversion count, trees
PROBLEM:
In a tree with N nodes, the S[i] for all nodes i are defined after running the following procedure:
val = 1
while the tree is not empty:
- Identify the nodes with degree > 2.
- Choose all the nodes having a path to a leaf node not passing through any node with degree > 2.
- Remove all of these chosen nodes from the tree.
- Set the S[i] value of all these removed nodes to be val.
- val += 1
You have to answer Q queries. Each query takes the form (u,v), and you have to compute the number of inversions in the list of $S[i]$s of all nodes in the path from u to v.
QUICK EXPLANATION:
Preprocessing:
- Compute the $S[i]$s in with the given pseudocode.
- Root the tree. Then for each node, compute its depth (distance from the root) and a pointer to its nearest ancestor with a different S[i].
- Preprocess the tree so for LCA queries.
To answer a query (u,v):
- First compute the LCA x.
- Then compute the sequence of $S[i]$s from u to x and from v to x, and then combine them to form the sequence of $S[i]$s. But instead of doing this by going up the tree one at a time, simply use the pointers to the nearest different S[i] to jump large gaps quickly. The array of $S[i]s, [s_1, s_2, \ldots], must be compressed as [(v_1, \text{count}_1), (v_2, \text{count}_2), \ldots]$ so it will stay short.
- Compute the inversion count in this array using the brute-force method.
This runs in O(\log^2 N), because the number of distinct $S[i]$s in any given path is O(\log N).
EXPLANATION:
Computing these S[i] things
To answer the question, we’ll most likely need to compute these $S[i]$s as the first step. Luckily, we were given a pseudocode, which is straightforward to implement, but a bit concerning since the running time might be slow.
Each iteration of the while loop takes O(N) time to finish. (Well, on later iterations, it takes lower because there are fewer nodes.) Thus, the running time of this procedure is O(N\cdot t), where t is the number of iterations. Let’s call t the tree’s niceness. But what is t? For the running time, we’re interested in finding an upper bound for t. Right now, we have the trivial upper bound t = \lceil N/2 \rceil, because any tree has at least two leaves, and leaves are removed at every iteration. But this gives us a running time of O(N^2) which is too slow. We’ll need a tighter upper bound for the niceness.
To find this bound, notice that this “niceness” thing is actually the subject of a problem used in a different contest. In the editorial for that problem, it is proved that a tree with niceness t has at least 3\cdot 2^{t-1} - 2 nodes. Thus, N \ge 3\cdot 2^{t-1} - 2, which is equivalent to t \le 1 + \log_2 \frac{N+2}{3}. So actually, t = O(\log N), and the running time of the procedure above is O(N \log N)!
So we now know that the procedure is actually fast. But there is a way to compute the $S[i]$s in O(N) time. The key to do so is to only visit removed nodes at every step. The details of this procedure are not that hard, so we’ll leave this to the reader.
$S[i]$s on a path
Now that we have the $S[i]$s, how do we go about finding the number of inversions in a sequence of $S[i]s in a path? In a random array, you might need \Theta (N \log N)$ time to do it. Doing this for all Q queries will take too long, so we try to find another way.
The key is to notice that the $S[i]$s are not random. In fact, there are likely to be many consecutive equal S[i] values. Furthermore, from the way the $S[i]$s are computed, they exhibit a very regular structure: The $S[i]$s only increase as we get “deeper” into the tree. In fact, nodes with the maximum S[i] are connected to each other, forming a single path!
If we try to root the tree in one of the nodes with maximum S[i], then any path from the root to a leaf is (weakly) decreasing. Since any path in this tree consists of an “upward” part and a “downward” part, then we find the following:
Any S[i] sequence in a path consists of two parts: a (weakly) increasing part and a (weakly) decreasing part.
For example, in the following tree, consider the bolded path. (The numbers in the nodes are the $S[i]$s.)
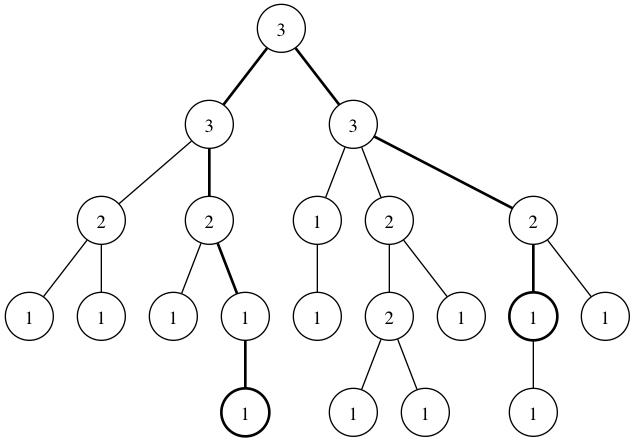
The sequence of $S[i]s is (1,1,2,3,3,3,2,1). This can definitely be split into two parts, (1,1,2,3,3),(3,2,1), where the first part is increasing and the second part is decreasing. (Note that the split is not necessarily unique. For example, (1,1,2),(3,3,3,2,1)$ is also a valid split.)
An array [s_1,s_2,s_3,\ldots] of this form is very nice, especially considering the fact that the number of distinct $S[i]$s is O(\log N). It means that there are 2\cdot O(\log N) = O(\log N) distinct maximal runs. If the array is represented in the form [(v_1, \text{count}_1), (v_2, \text{count}_2), (v_3, \text{count}_3) \ldots], then computing the number of inversions is easy and can be done in O(\log^2 N)!
So all that remains is to compute the “(value,count) array”.
Note: Actually, computing the inversion count can be done in O(\log N), by using the fact that for every i, the set of indices j forming an inversion pair with i forms a suffix of the array. We’ll leave it to the reader to find this O(\log N) method.
Computing the array
Given nodes u and v, our task is to find the (value,count) array of the path from u to v. Here, we assume that the tree is rooted (arbitrarily).
We can actually compute the “upward” and “downward” parts separately, by first computing the lowest common ancestor (or LCA), say x. The “upward” part is from u to x, and the “downward” part is from x to v. These are both instances of the same task, but one of the nodes is an ancestor of the other, so in the following we may assume that one of u or v is the ancestor of the other. Afterwards we can just combine them to get the whole array. (Don’t forget to count x itself only once!) Computing the LCA itself will only take O(\log N) with an O(N \log N) preprocessing.
So our task is to find the (value,count) array of the path from u to v, assuming one of them is the ancestor of the other. Without loss of generality, assume v is the ancestor. If not, then we can swap u and v, then reverse the (value,count) array.
Now, walking the tree upwards by following the “parent” pointer is probably too slow because the path can be very long. But since we only want the (value,count) array, all we really want is to know the nearest ancestor of the current node with a different S[i] (or null if all nodes up to the root have the same S[i]). But these special ancestors can be computed in O(N) time using a simple traversal! Namely:
diff_anc[1..N]
diff_anc[root] = null
for all nodes i != root in preorder (or levelorder):
p = parent[i]
if S[i] == S[p]:
diff_anc[i] = diff_anc[p]
else:
diff_anc[i] = p
This uses dynamic programming on the tree to compute diff_anc[i] for all i. In addition, we also need to know the distance between i and diff_anc[i] in order to know the “count”. This can be done with a similar dynamic programming. Or it can be done by computing the depth of each node (the distance from the root), so that the distance between i and an ancestor a is \mathop{depth}(i) - \mathop{depth}(a).
Thus, we can now compute the count array in time proportional to the length of the array, or O(\log N)!
Time Complexity:
O(N \log N + Q \log^2 N)
AUTHOR’S AND TESTER’S SOLUTIONS:
[setter][333]
[tester][444]
[editorialist][555]
[333]: The link is provided by admins after the contest ends and the solutions are uploaded on the CodeChef Server.
[444]: The link is provided by admins after the contest ends and the solutions are uploaded on the CodeChef Server.
[555]: The link is provided by admins after the contest ends and the solutions are uploaded on the CodeChef Server.