CHEFPOLY - Editorial

editorial
, , ,
1

Problem Link:

Practice
Contest

Author: Misha Chorniy
Tester: Pushkar Mishra
Editorialist: Praveen Dhinwa

Difficulty:

medium

Pre-Requisites:

geometry

Problem Statement

You are given R red and B black points in a 2-D plane. All the points in the input have distinct coordinates. Also, no three points are collinear. You will be given some queries, each containing a convex polygon whose vertices are some of the red points and you have to find the number of black points inside that polygon.

Explanation

Note that the problem states that no three points among all the given R + B points would be collinear. This condition ensures that no black point will lie on a side of the polygon. Either it will lie strictly outside or strictly inside the polygon.

Subtask 1

N is fixed to 3. So, the polygon given in the query will be just a triangle made by the given 3 red points. So, we just have to find the number of black points inside this triangle. We can iterate over each of the black points and check whether it lies inside the triangle or not.

Time complexity of this algorithm will be O(B) \, \times \, \text{time taken in checking a point lies inside a triangle or not}. Checking whether a point lies inside a triangle can be done in constant (O(1)) time. So overall time complexity will be O(B).

Subtask 2 and 3

For a query polygon, we will iterate over each black point and will check whether it lies inside the polygon or not.

We can test whether a point lies inside a convex polygon via many techniques in O(n) time where n denotes the number of points in the polygon. Please see the following links for learning more about these techniques

So, we answer a single query of a polygon of size n in O(n * B) time . So, answering all the queries will take time O(\text{sum of number of points over all the queries} * B).

Now, this solution won’t solve the highest subtask. We can’t afford to have a factor of B in time complexity of a query. What if we could smartly precompute something so that we can answer each query in size of polygon (i.e. O(n) time) itself.

Subtask 4

Concept of vector area
If you know the method of finding area of polygon by the use of concept of vector area, then you can tackle the problem of finding number of black points inside a polygon in a similar way. So, let us try to understand the approach for finding area of polygon.

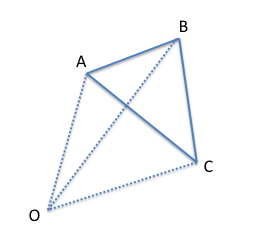
Drawing

Let us take an example of a triangle \Delta ABC such that points such that A, B, C are in clockwise order, as shown above. We want to find its area.
Let O denote a point which we will assume that lies outside the given triangle.
Note that we can write the area of the \Delta ABC as area(\Delta OAB) + area(\Delta OBC) - area(\Delta OCA).

Now, let us understand the concept of area as a vector. Please see the following link for a fun reading about this topic. For a \Delta PQR, its vector area will have same magnitude as that of usual area, but it will also have a direction which will depend on the sign of cross product (P,Q) \times (Q,R).
Direction of cross product of PQR ((P,Q) \times (Q,R)) will be perpendicular to the plane of your screen. If the cross product has direction going inside the plane, then we will denote it by having positive sign and negative sign otherwise. e.g. cross product of OAB, (OA \times AB) will be having positive magnitude whereas OCA, (OC \times CA) will have negative magnitude.

Now, we can notice that \Delta area(ABC) = signedArea(\Delta OAB) + signedArea(\Delta OBC) + signedArea(\Delta OCA).
Voila, Did you notice that we did not have the need of putting minus sign anywhere in the formula?
It is due to the fact that signedArea(OCA) = - area(OCA) because the direction of cross product of OCA is coming out of the plane, which we considered to have negative sign.

This approach can be generalized to any polygon in this way. Let P denote the convex polygon with its points arranged in clockwise order. We will iterate over each of the two consecutive sides (P_i, P_{i + 1}) of it and add the signedArea(\Delta O P_i, P_{i + 1}) into our answer.

You can also note that the condition of point O lying outside the polygon can also be dropped altogether. This is left as an exercise to think about.

Use this concept to solve our problem
So, in our problem, instead of finding area of a polygon, we have to find the number of black points inside a polygon. In our case, we can use the same approach with a modification that now area will denote the number of black points inside a polygon.

In the pre computation step, we will iterate over each pair of red points P_1, P_2 and find the number of black points inside the triangle \Delta O P_1, P_2. There are total O(R^2) such triangles. For each triangle, we check for each of the black points lies inside the triangle or not. Total time taken in this pre-computation step will be O(R^2 * B).

Now, after doing this preprocessing step, we will be a given query polygon. We can answer such a query by using the approach described to find area of a general polygon. Using this approach, we can answer a query of a polygon of size n in O(n) time.
So, total time will be sum of n over all the queries.

Overall time complexity of this approach is O(R^2 * B + \text{sum of sizes over all query polygons}).

Solution:

Setter’s solution can be found here
Tester’s solution can be found here

Please feel free to post comments if anything is not clear to you.

2

please update all links as all of them points to cook67.

3

Setter’s solution - http://ideone.com/biHz9k

Tester’s solution - http://ideone.com/EJOhDb

4

Alternate Approach

One can precompute for every pair of red points , the set of black points lying strictly on the left of the line joining these 2 red point with y coordinate between y coordinate of these 2 points and same for the right of the line as well.

Now a point will lie inside a polygon if and only if it lies on strictly left of any one line joining 2 consecutive points of polygon as well as strictly right side of any line joining 2 consecutive points.

So now we just need to merge all the sets of left side points and the rightside points and take the intersection of these 2.
This can be done using bitsets where the complexity of intersection and union is O(M/32) so the overall Complexity becomes O(N^2 * M * M / 32) Precomputation and O(K * M / 32) per query.


[1]


  [1]: https://www.codechef.com/viewsolution/9500240
5 Likes
5

In both the codes the red and black points have been offset by a large number to make both the co-ordinates positive. Why is this necessary ?

6

This is Misha’s solution explanation by him.

  1. Add for each point (10^4+1, 10^4+1), now all points lie in first quadrant (x > 0, y > 0).
  2. Let for each pair red points (Ri, Rj) define next value F[i][j]
    F[i][j] = number of black points which lie inside triangle (Ri, (0, 0), Rj), if polar angle Ri less or equal then polar angle Rj.
    And F[j][i] = -F[i][j], otherwise.
    So answer for polygon (i1, i2, …, ik) is abs(F[i1][i2] + F[i2][i3] + … + F[i_{k-1}][i_{k}] + F[i_{k}][i1]), if and only if black point lie inside polygon,
    we count it.
7

Nice solution :slight_smile: Kudos :slight_smile:

8

I have understood the solution, but what is the need of adding (10^4+1, 10^4+1) to each point?

9

@foraml fewer cases

10

Please explain
1.const int MaxN = 3e3 + 10
(Why we add it with white[] points).
2. if (inTriangle(white[i], zero, white[j], black[k]) == true) {
cnt[i][j]++;}
(passing zero ?)
3. cnt[j][i] = -cnt[i][j];(What is use of this step?)