CCRICLES - Editorial

[anand20]

Problem Link :

Division 1

Division 2

Author : Smit mandavia

Tester : Misha Chorniy

Editorialist : Anand Jaisingh

Pre-Requisites :

Basic Geometry

Problem :

For N circles on the 2-d co-ordinate planes, you need to find the minimum and maximum distances between 2 points one from each circle, and then answer some queries.

Explanation :

First of all, this problem was only for Division 2, but IMO this problem is much better than some of the problems that were only in Division 1. So, don’t feel too bad if you couldn’t solve this problem.

Basic knowledge of circles and lines is required to solve this problem. First of all, it may be evident from the constraints that we cannot process each K individually for each pair of circles. It may be much more profitable to do some kind of pre-processing so that we can later answer queries in something like O(1) or O(log_{2} (N^2) ) .

Let’s try and think of a single pair of circles for a moment, and forget everything else.Take a pair of points having maximal distance between them , one from the first circle, the other from the second.Now, take the pair of points where is distance is minimal

Taking any pair of points that are not equal to any of these 2 pairs, we know that the distance between them can only lie in the closed interval [minima,maxima]. In fact, if can be proved that for each real x, such that x lies in the interval [minima,maxima] there exists a pair of points having distance between them equal to x.

Now, if we can find the minima and maxima of the distances for 2 circles, then we can answer queries rather easily.

However, to do the former requires some case processing :

Big Hint : Try and draw a line passing through the centers of both circles, and analyzing this will lead you to all answers. In fact, it can be proved that the maxima is always the sum of the distance between the centers of the 2 circles and their radii. For example, consider :

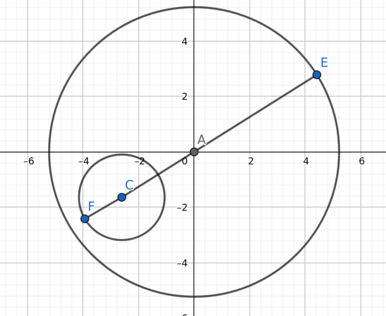
Here, the length of segment FC is the radius of the inner circle, the length of segment CA is the distance between the centers of the 2 circles, and the length of segment AE is the radius of the outer circle.

So, |FE| = |FC|+|CA|+|AE|

We can prove this similarly for the cases when the circles only partially intersect, or don’t intersect at all. Now, for the minima, cases :

A. : The two circles share no common points

The minima in this case is the distance between the centers of the 2 circles minus the sum of their radii.

B. : A part of each of the circle intersects with the other

The minima here is obviously 0 as the 2 circles share at least 1 common point

C. : One of the circles lies completely inside or on the boundary of the other circle.

This is a tricky case. Here it’s the radius of the larger circle-(radius of the smaller circle + distance between the centers of the 2 circles). We can prove this as follows :

Let the radius of the outer circle be r. Any point on the outer circle’s circumference is at exactly a distance of r from the center of the outer circle. Now, if we can find the most distant point on the circumference of the inner circle from the center of the outer circle, then we can subtract that distance from r to get what we want. Now, that maximum distance is the distance between the centers of the 2 circles + the radius of the inner circle.

We can visualize this via the following image :

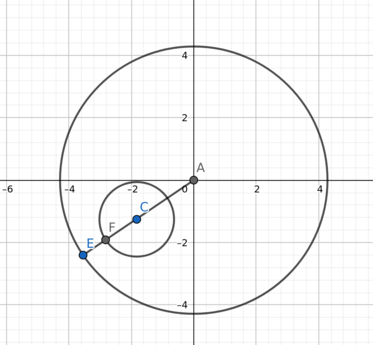
Here, point F is the most furthest point from point A, and the length of segment AF is length of segment AC i.e distance between the centers + length of segment CF i.e the radius of the inner circle. Now, length of segment i.e. |FE|=r-|AF| .

Now, to find if 2 circles intersect, overlap completely or don’t intersect at all is a problem that has appeared before. You can solve this problem to understand this part, and read the problem’s editorial if necessary.

Now, for a pair of circles once we found the maxima and minima, for each integer x such that x lies in the interval [minima,maxima], we can increment the answer for x by 1. However, to prevent looping, we can use the answer[minima]++, answer[maxima+1]-- trick since we can answer all queries offline.

Later, we can just print answer[k] in O(1). Overall time complexity : O(N^2+maxK+Q), where maxK=10^6.

Author’s Code : Link

Tester’s Code : Link

My Code : Link

[thedeadlegend]

So, this brilliant question could indeed be answered using basic circle knowledge. Just wanted to know if one could consider two circle pairwise and follow the given pattern for the rest of the solution?

[thesmartguy]

Awesome editorial! Thanks for uploading it so early. :))

[jagreetdg]

Another could be taking up a calculas based approach. Take the parametric equation of the two circles, get distance equation of the two circles and differentiate the equation to get the minimum and maximum distance between the two circles and hence include all values of k between min and max distance. This way different positions of circles won’t have to be considered as different cases. I haven’t personally coded this solution, but this should work theoretically.

[code_report]

Video solution with explanation: https://youtu.be/oDJQU9wxxRM

[music]

Since all the solutions seem to be taking sqrt for calculating the distance between the centers. Why we don’t have double precision issues here? Can we solve this problem without any double calculation?

[sagar2405]

After finding minimum and maximum pair for each circle pair, i used two technique to answer the query:

1. declare a array d[1000001]={0}, and for each pair, increment the value of d[i], i ∈ (minimum(i’th pair),maximum(i’th pair)).
2. Another way is store each min,max pair in vector of pair. Then sort according to minimum distance and apply linear search for each query.

But i get tle in both case, how can i do query part more efficiently?

[blackerror]

why this is wrong ? . link https://www.codechef.com/viewsolution/20851748

[thesmartguy]

abhijeet_kr refer to this problem of Array Manipulation in Hackerrank…Array Manip. It will help you in understanding your doubt.

[abhijeet_kr]

okay!! thanks @thesmartguy

[l_returns]

Because you just need very less precision to get AC as you are just concerned about the floor and ceil value of the distance… nothing else… As the inputs are integer… My solution don’t contain double data type anywhere…(obviously I am calculating sqrt once) So solution seems to be comparatively more faster when we don’t use double.

[l_returns]

It was only a basic circle geometry… nothing else…

[l_returns]

Use a smart way to update each of values from min to max…
i.e. one of the technique could be…
d[min]++;
d[max+1]–;
For each pair of circle…
Then do
d[i]+=d[i-1]
For each index in d…
This will create the similar array which you created with very less time complexity and it won’t go for TLE…

[sudhanshuom199]

Why this code is giving tle??? I don’t understand. My approach is same as the explanation. Please tell.

import java.util.*;

class Solution {

static final Scanner sc = new Scanner(System.in);

public static void main(String[] args) {
    int n = sc.nextInt();
    int q = sc.nextInt();
    int max = 1000000;
    int ar[] = new int[max];
    int qq[] = new int[q];
    double arr[][] = new double[n][3];
    int tot = n*(n-1)/2;
    double ds[][] = new double[tot][2];
    for(int  i=0 ; i<n; i++){
        arr[i][0] = sc.nextDouble();
        arr[i][1] = sc.nextDouble();
        arr[i][2] = sc.nextDouble();
    }
    for(int i = 0; i<q ; i++){
        qq[i] = sc.nextInt();
    }
    int in = 0;
    for(int i = 0; i< n-1; i++){
        for(int j = i+1; j<n;j++){
            double x = Math.pow(( Math.pow( (arr[i][0]-arr[j][0]), 2) + Math.pow( (arr[i][1]-arr[j][1]), 2)), 0.5);
            if(x >= arr[i][2]+arr[j][2]){
                
                ds[in][0] = x - arr[i][2] - arr[j][2];
                ds[in][1] = x + arr[i][2] + arr[j][2];
                ar[ds[in][0]>(int)ds[in][0]?(int)ds[in][0]+1:(int)ds[in][0]] += 1;
                if((int)ds[in][0] < max-1)
                    ar[(int)ds[in][1]+1] = ar[(int)ds[in][1]+1] - 1;
                in++;
            }
            else if((x + arr[i][2]<arr[j][2]?arr[i][2]:arr[j][2]) <= (arr[i][2]>arr[j][2]?arr[i][2]:arr[j][2]) ){
                
                ds[in][0] = (arr[i][2]>arr[j][2]?arr[i][2]:arr[j][2]) - x - (arr[i][2]<arr[j][2]?arr[i][2]:arr[j][2]);
                ds[in][1] = 2*(arr[i][2]>arr[j][2]?arr[i][2]:arr[j][2]) - ds[in][0];
                if(ds[in][0]<0){
                
                    ds[in][0] = 0;
                    ds[in][1] = x+arr[i][2]+arr[j][2];
                }
                ar[ds[in][0]>(int)ds[in][0]?(int)ds[in][0]+1:(int)ds[in][0]] += 1;
                if((int)ds[in][0] < max-1)
                    ar[(int)ds[in][1]+1] = ar[(int)ds[in][1]+1] - 1;
                in++;
            }
        }
    }

    for(int i = 1 ; i < max; i++){
        ar[i] += ar[i-1];
    }
    for(int ii = 0; ii < q ; ii++){
        if(qq[ii]<max){
            System.out.println(ar[qq[ii]]);
        }else
            System.out.println("0");            
    }
    
}

}

[anand20]

Did you try using fast input too ? Scanners and System.out.println can be quite slow.

[sagar2405]

Thanks @l_returns4, its working.
I think you should write a blog on such tricks, this help many beginner.

[l_returns]

Okay I ll try… U r welcome

[l_returns]

Avoid using double data type more… it’s not needed as per my solution… I ll upload authors solution today… Have a look… Avoiding using double will make your code fast… Mine runs in 0.06 in c++

[l_returns]

I have integers everywhere…

[l_returns]

And I agree with @anand20 too… Mine is just one more optimization advice…