PROBLEM LINK:
Setter: Bogdan Ciobanu
Tester: Lewin Gan and Istvan Nagy
Editorialist: Taranpreet Singh
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Binary Lifting would do.
PROBLEM:
We have a tree consisting of N vertices rooted at 1 and N cats. We are also given the permutation determining the vertex ith cat shall try to jump. The cats arrive in order only. When the cat reaches the p_i vertex, it tries to climb up as much as possible and stops only when the next ancestor is already occupied. For each cat, determine the number of jumps made by that cat. Initial jump to vertex p_i also counts as a jump.
QUICK EXPLANATION
- Initially, when checking for the ith cat, first check if the p_i vertex is occupied already, in which case the number of jumps for this cat is zero. Otherwise, it reaches vertex p_i in one jump. It can be done using a boolean array.
- Observation is, that on the path from any vertex to root, there shall be some vertices from root to some ancestor of the vertex which are occupied and all others are empty. We need to find the number of jumps required to reach first empty vertex out of these.
- We can preprocess to find out $2^i$th ancestors of every node (-1 if it doesn’t exist). So, we can check $2^b$th ancestors (b in decreasing order and making a binary jump to the 2^b ancestor of the current node.
EXPLANATION
First of all, we need to check if the cat even manages to make the first jump to the vertex p_i. That can be checked by making each position available or occupied in a boolean array. If the position a cat wants to jump to is already occupied, the answer is zero, since the cat cannot make even a single jump. (Sad Life:( ).
Assuming it manages to make its first jump. Now, it starts its climb upwards. If we consider the path from p_i to root, we get all the ancestors of p_i, one of which shall be the final position of the cat, from where the cat cannot move upward. It can be noticed that since the cats always try to move upwards, there will be some ancestors near the root which would be filled, the remaining ancestors being empty. We use binary lifting here.
Suppose we know, that the final destination node is at distance at most 2^B from the current node. Suppose we check 2^{B-1} parent of the current node. If the node is occupied, all nodes above it are occupied too and then, we are guaranteed to have the final node at distance at most 2^{B-1} from the current node. If the node is empty, all nodes below it are empty and the final node is at distance at most 2^B - 2^{B-1} = 2^{B-1} from 2^{B-1} ancestor of the current node. So, after checking for 2^x ancestor, we can check for 2^{x-1} ancestor and so on, and moving upward whenever we find an empty node. It is can be easily seen that the cat shall end up at the uppermost empty node it can reach. This is what we seek.
See the image. (Assuming all the nodes on the path of root to the current node, with root on top).
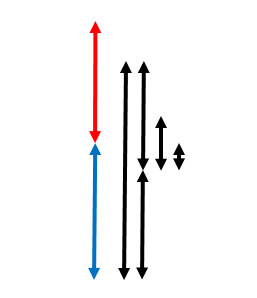
In the image, the red segment reflects occupied vertices and blue segment reveals the empty ones.
The first black segment is checking some 2^x ancestor of the current node which is occupied. We do not move the current node.
The second black segment checks 2^{x-1} ancestor of the current node, which is empty. It moves up to say vertex X.
The third black segment starting from node X and tries 2^{x-2} ancestor, which is occupied. No move occurs.
The last black segment tries 2^{x-3} ancestor of X and moves up. We can see that it has reached the uppermost node it can.
Time Complexity
Both Time and Memory complexity are O(N*log(N)).
AUTHOR’S AND TESTER’S SOLUTIONS:
Setter’s solution
Tester’s solution
Editorialist’s solution
Feel free to Share your approach, If it differs. Suggestions are always welcomed. 