Cannot understand Chef and Brackets

general
1

PLease if anyone could explain me the DP approach of the question Chef and Brackets as I am not able to understand the solution from the editorials.

Please explain so that a beginner like me could understand.

2 Likes
2

In that problems, I solved with back-tracking, with same complexity : O(n * 2^n * k), which is easier to understand and install :slight_smile:

3

Ok I’ll try to explain it in a really simple way.

The first step of solving dynamic programming problems is that you start thinking in a recursive manner. Hows that done you may ask !.

  1. Assume that by time travel(5D->blackhole->3D) you have a solution already. In this case lets say you have an array of numbers and you already know the solution for brackets problem for this array. Lets call this array as 
    arr[0,N-1] Or arr[i,j] if you like to generalize
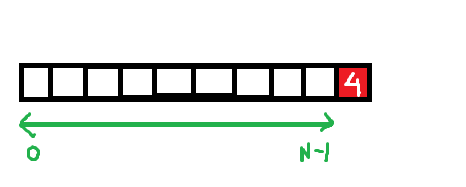
  2. Ask your self- What the chuck would happen if I add one cute little number to the end of this array. No big deal …just a number. So here is the thing… array and a new number added to the end of it…(new number = 4).alt text
  3. Lets say answer for this array was 
    S[0,N-1]
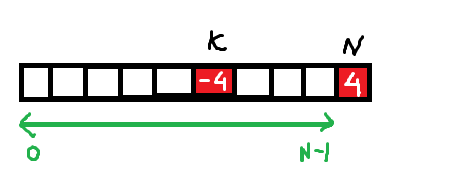
  4. Now try to understand what can happen when you add 4 to the end of this array. This ‘4’ will form a bracket with any ‘-4’ present in the array right?. Lets put a -4 somewhere. alt text

Now this newly added 4 will form a bracket with this ‘-4’. So total brackets in this new array (arr[0,N]) is solutions for old one + 1. 

S[0,N-1] + 1

Now thats not the only new bracket that got created. If you see carefully all the brackets in the region [k+1,N-1] can now be put inside the {-4,4} bracket. Like this-> 
 -4 {} 4

So our new bracket count becomes- 
 S[0,N-1] + 1 + S[k+1, N-1]

Correct…Now what else…All the brackets in the region S[0,K-1] can now be coupled with all of these new brackets to create new brackets. Like-
{-A A}{-4 4} OR

{-A A}{-4 {} 4} . . .

So our new bracket count becomes-
S[0,N-1] + 1 + S[k+1, N-1] + (1+S[k+1,N-1])*S[0,k-1]

Because all the brackets in region (0,k-1) can go with the newly created (1+S[k+1,N-1]) brackets. Thats why we used multiply. So total count now becomes(What a mess by just adding one number eh? :D)


S[0,N-1] + (1 + S[k+1,N-1]) * (1 + S[0,K-1])

Thats it…pHew…but wait…what will happen if we have multiple '-4’s ???. Well, we will repeat this process for all those -4’s.
  1. Now lets generalize this thing and write a formula-
    S[i,j] = S[i,j-1] + (FOR all k such that arr[k] == -arr[j]) (1+S[i,k-1])*(S[k+1,j-1]+1)

Now you have successfully created a recurrence relation. Second step is how to write dynammic programming code for this thing. If you see that to calculate value for a range [i,j] you require values of ranges [i,k-1] and [k+1,j-1] which are definitely smaller ranges when compared to [i,j]. So while writing dp code for this what you have to do is find values of all the small ranges before proceeding to the bigger ranges. Which in lay man terms means->

  1. Find values for ranges [0,0], [1,1], [2,2], [3,3] …[i,i]…[N-1,N-1]
  2. Find values for ranges [0,1], [1,2], [2,3], [3,4], …[i,i+1]…[N-2,N-1]
  3. Find values for ranges [0,k], [1,1+k], [2,2+k]…[i, i+k] …[N-k-1, N-1]
  4. do it for [0,N-1] and we are done!

Here is the link to my solution-Show me the code, talk is cheap

PS: There are some corner case checks in the code. Play around them to understand what they do.

PS2: Code might or might not be perfect, deal with it.

39 Likes
4

Think this manner: For DP to be applicable we need two things, Optimal substructure and overlapping subproblems. If we talk about optimal substructure, then finding the number of valid brackets in a range say (i,j), we need to find the summation and all permutations(with this i,j) of all valid brackets of the ranges that lie within (i,j). Thus, we can obtain Optimal solution for(i,j) by using optimal solutions to all the subranges. If we talk about overlapping property, lets say, a closing bracket of ith value occurs at some index k<j. We need optimal solution of (k,j) for our calculation. This subproblem may be required for some other (i’,j’) calculation when a[i’]=a[i] and i’<j. Hence, the two conditions satisy and we can now apply DP.

Here is my solution based on the DP explained in editorial. Basically we are pre-computing the number of valid brackets in the range (i+1,j) . Two possibilities arise here: include the bracket at i’th position or don’t include. Now, for (i,j), the number of valid brackets are all that are in the range (i+1,j) + v where v for the time being is a variable(used when we include the brace at i’th position). When we are not including x, then we are not including the bracket at the i’th position. But if we include, let the bracket at i’th position be the opening brace(no need when a[i]>0 i.e. closing brace) of type x(i.e. -x). Then we need to know where in the range of (i+1,j) we have a closing brace of type x. We include all these combinations i.e. v= m[i+1,k]*m[k+1][j] where k belongs to [i+1,j] and a[i]<0 && a[k] + a[i]=0.

1 Like
5

Thank you so much for such an elaborate explanation…:slight_smile:

1 Like
6

Thank you so much for the explanation

7

applause. Such a well thought && entertaining explanation. you should write a book or something.

5 Likes
8

glad to help :slight_smile:

1 Like
9

beautifull answer … :slight_smile:

10

S[0,N] + 1 + S[k+1, N-1] Shouldn’t it be S[0,N-1] +1 +S[K+1,N-1]?

11

@damn_me- Yes, my bad. Corrected the typos

12

This is going to help me in visualising all DP problems in future :slight_smile: Thankyou!

13

@nitinj Can you please elaborate on the corner case checks. I get how the code works, but can’t quite figure out all the if-else checks. Thanks!

14

hey rick93 check this solution->

http://www.codechef.com/viewplaintext/5615785

I’ve removed extra unnecessary if conditions. The only condition checks for the case where k=i

15

_/_ nice work bro