CAKE1AM - Editorial

editorial
, , ,
1

PROBLEM LINKS

Contest

Practice

Author: Abdullah Al Mahmud

Tester: Gerald Agapov

Editorialist: Praveen Reddy Vaka

DIFFICULTY:

cakewalk

PREREQUISITES:

Basic Coordinate Geometry

EXPLANATION

Restated in simple terms the problem asks for the area of the union of rectangles. Let us call the rectangles R1 and R2. A rectangle is represented by two points (x1, y1) its bottom left point and (x2, y2) its top right point.

If the rectangles don’t intersect the answer would be simply sum of areas of the individual rectangles. If they intersect then we need to subtract the intersecting area as we account for this area twice in the sum. So the answer is simply area(R1) + area(R2) - intersectingArea(R1, R2).

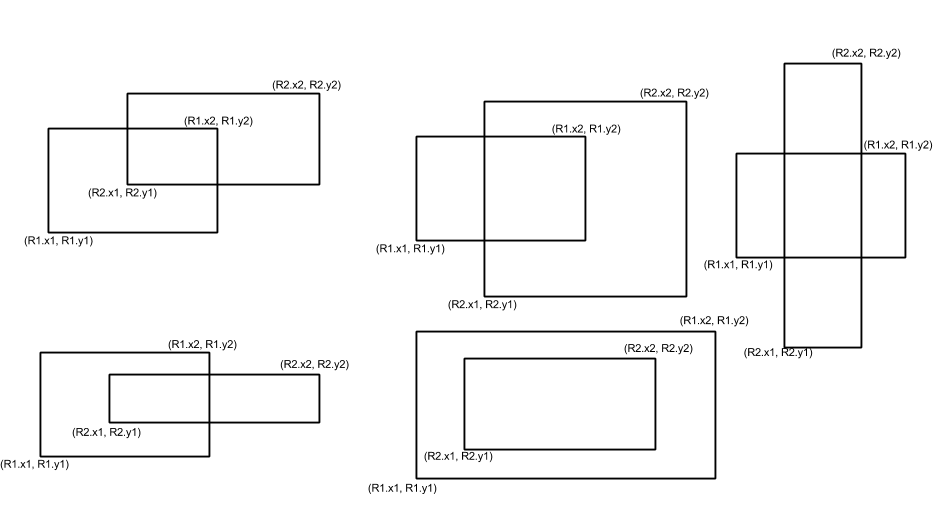
Let us now look at how to find if the two rectangles are intersecting and the area of their intersection. First let us consider just the case when the rectangles intersect. Here is a diagram showing some possibilities of rectangles intersecting.

Rectangle%20Intersection.png940×505

Based on these figures it can be easily observed and also proved for any general case that if the rectangles intersect the lower left point of the rectangle representing the intersecting area is (max(R1.x1, R2.x1), max(R1.y1, R2.y1)) and the top right point is (min(R1.x2, R2.x2), min(R1.y2, R2.y2)). Once we find these points we can find the area of the intersecting region also. Note that the rectangles R1 and R2 are interchangeable it doesn’t matter which one is seen as the first rectangle.

To check if the two rectangles intersect in the first place it is as simple as finding these two points and see it they form a well defined rectangle. If they form a well defined rectangle they intersect otherwise they don’t. Let us call the two points (R3.x1, R3.y1) and (R3.x2, R3.y2), they form a well defined rectangle only if (R3.x1 < R3. x2) and (R3.y1 < R3. y2) as both coordinates of bottom left point have to come before the corresponding coordinates of top right point.

SOLUTIONS

Setter’s Solution: CAKE1AM.cpp

Tester’s Solution: CAKE1AM.cpp

9 Likes
2

I had a pretty simple bruteforce solution. Initially set the area to be 0.
For each coordinate (x, y) (where x >= 1 && x <= 1000, y >= 1 && y <= 1000), Check whether this coordinate lies in any of the rectangles, If yes then increment the area.

4 Likes
3

I have also implemented the above method but i doubt as to why this solution passed because in worst case we will be doing 10^6 operations per test case and 10^8 operations for all test cases as T<=100 so probably it should get TLE but it doesn’t so the test cases were not made that strict .

1 Like
4

very nicely explained

5

Exploiting the problem constraints really nicely! :smiley:

6

Problem setter’s code is not working. The code is not even compiling. What crap is written in that?
“>?” operator in C++??

7

With Codechef moving to Cube Cluster, 10^8 operations per second get performed easily, hence the code is getting accepted.

1 Like
8

@ashishiti I am not really sure about that. I didn’t have to access to this particular solution of setter, I had access to others so couldn’t verify this. Maybe something went wrong somewhere. I have informed the setter. Hope he will get back soon.

9

I guess the constraints were deliberately set to have such solutions accepted, I have not discussed this point with setter so I can only guess. As Ankit pointed out you can run close to 10^8 operations in a second on cube.

1 Like
10

I solved in the same way :smiley:

11

I was using some deprecated operator instead of MIN and MAX, which were not compiling in codechef.