PROBLEM LINKS
DIFFICULTY
EASY
EXPLANATION
SETTER’S SOLUTION
Can be found here.
TESTER’S SOLUTION
Can be found here.
1 Like
If k elements from both ends are fixed, then we can do it in k+1 ways and we have to permute n-k remaining elements i.e. q(n-k)(k+1)/n! or if n-k elements are fixed, which can be done in n-k+1 ways, then we permute k remaining elements i.e. q(k)(n-k+1)/n!. The formula is correct but the explanation is wrong. The editorial is as confusing, if not more, as the problem statement.
6 Likes
Hi, I think the general idea for calculating the required expectation can be expressed as:
E(n) = 1 + (probability of outcome 1 * expected number of steps to reach the goal after outcome 1 has happened) + … (same for rest of the outcomes)
It can be considered as analogous to the problem of random walks.
So, I think the correct formula would be the following:
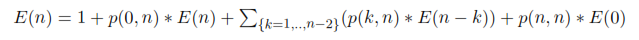
where E(n) is expected number of shuffles to sort n numbers using the procedure described in the question.
p(k,n) is the probability that a total of k out of n elements that are present at the ends are placed at the right places after the initial shuffle.
p(n,n)*E(0) is essentially 0 because E(0) is 0.
Note: The event where n-1 elements out of n elements are in right place is exactly same as the event where all elements are in the right place. So, E(1) = E(0) = 0. So, I counted only upto n-2 in the above formula.
1 Like