BEAUTGAR - EDITORIAL

general
, , , ,
1

PROBLEM LINK:

Practice
Contest: Division 1
Contest: Division 2

Setter: Praveen Dhinwa
Tester: Teja Vardhan Reddy
Editorialist: Taranpreet Singh

DIFFICULTY:

Simple

PREREQUISITES:

Observations.

PROBLEM:

Given a garland represented by string S consisting of two colored flowers Red and Blue, determine, whether we can attain a beautiful garland, defined as a garland having no two consecutive flowers of the same color, by applying the following operation at most once.

Make two cuts on garland to obtain two parts, reverse one and join it back.

SUPER QUICK EXPLANATION

  • Only even length garlands with the same number of red and blue flowers have the possibility of being a part of beautiful garland, except garland of length 1.
  • Such garland is beautiful, if the number of positions having current character same as next character, is either zero or two.

EXPLANATION

Let us see a beautiful garland first.

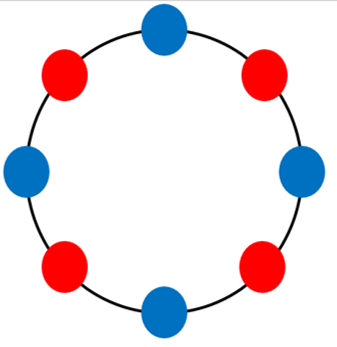
alt text

Let us consider a garland of length 1. We know, it has only one flower, so it can never have two consecutive flowers of the same color, hence, is a beautiful garland. We answer yes in this case.

Now, we have garland length \geq 2.

Now, we need to end up with a beautiful garland, which, we can notice, has the same number of red and blue colored flowers. Hence, the garland, which does not have the same number of flowers can never end up as a beautiful garland, even after performing operations.

This way, all garlands we are left with are the garlands of even length (simple to prove) having the same number of flowers of both colors.

First of all, check if the garland is already beautiful and report if it is. Now, we are left with a non-beautiful garland and we have to make a cut, trying to make it beautiful.

Let us understand the consequence of performing the operation. See, we make the cut, reverse a string, and attach it back. Except for border flowers of both pieces of garland, the rest of the flowers continue to have same adjacent flowers as before.

Consider an example RRGGRRGG. We make first cut between first and second flower while the second cut between seventh and eighth flower. The resultant garland becomes RGRRGGRG. We see, that only pairs of positions around both cuts are affected by the operation.

Hence, if we call a pair of adjacent same-colored flowers as mismatch positions, then, we can prove, that we can remove exactly two mismatches using one swap.

See, since only the two pairs of positions enclosing either of the cut are affected by a cut, we cannot remove more than 2 mismatch positions using one operation.

This way, the solution is just to count the number of mismatch positions in garland, and we can make the garland beautiful, if there are either zero or exactly two mismatch positions, after handling the case of garland consisting of a single flower.

Exercise

Prove that the number of mismatch positions in an even length garland having the same number of both colored flowers, cannot have an odd number of mismatch positions.

Time Complexity

Time complexity is O(|S|) since we iterate over the string.

AUTHOR’S AND TESTER’S SOLUTIONS:

Setter’s solution
Tester’s solution
Editorialist’s solution

Feel free to Share your approach, If it differs. Suggestions are always welcomed. :slight_smile:

4 Likes
2 
Let us consider a garland of length 1. We know, it has only one flower, so it can never have two consecutive flowers of the same color, hence, is a beautiful garland. We answer yes in this case.

Length of garland is at least 2 in the question :p. Good that you told about the case though, because many times I have seen people get confused in such cases (one case in point is case of N=1 in Beautiful Array)

A very good exercise would be, to prove that, if we can do the operation infinite times, we can always make the garland beautiful if it has equal R and G's

(Hint: Try obtaining string of form RRR...GGGG... and proceed henceforth.)

1 Like
3

My try at the exercise:

Let’s call contiguous same-coloured flowers a block. So, e.g., blocks will look like R, RRR, GG etc. My proof assumes that the maximum length of any block of flowers in the garland is 2. So the garland may look like RRGRGGRG etc.

Let the number of blocks of red flowers of length 1 be R_1 and of length 2 be R_2, and similarly for green flowers, let the numbers of blocks be G_1 and G_2 respectively.

Since the garland is made of alternating red and green blocks, the number of red blocks is equal to the number of green blocks, i.e.,

R_1 + R_2 = G_1 + G_2

Also, since the number of red and green flowers is equal, we have

R_1 + 2R_2 = G_1 + 2G_2

Solving the above equations, we get R_2 = G_2, i.e., the number of red and green blocks of length 2 is the same. So, the total number of blocks of length 2 is 2R_2 (or 2G_2), which is also the total number of mismatch positions. Hence the total number of mismatch positions is even.

1 Like
4

I missed the “equal colours” criterion because I was thinking about the general problem with unlimited different colours. So when I modified it to just red and green for the competition it was a little clumsy.

The unlimited-colours solution requires that
(a) there are no more than two pairs
(b) if two pairs, they are different colours
© if only one, there are two consecutive flowers somewhere neither of which is the pair colour.

© is a little tricky, but can be tested (by the pigeonhole principle) by checking that the pair colour isn’t dominant; that is, accounts for not more than half of the flowers. So a garland like GRBRYRR can’t be made beautiful - every cut has R on one side, so the R pair will always survive. And of course it has 4 R out of 7 flowers.

My solution to this extended problem

2 Likes
5

Won’t the exercise is proved by the following statement :

If we start with a mismatch and then move on taking alternating flowers , we are bound to make one more mismatch so that the count of R and G is same .

For example , let us begin with

RR , Now

RRG , //R is one more than G

RRGRG, //R is one more than G

RRGRGG //We will have to make another mismatch to equalise R and G!

Similar string will be obtained in case we get a mismatch in between or with the pair s[0] and s[n-1].

1 Like
6

Quite an overkill for this problem. :slight_smile:

1 Like
7

I thought the same thing :smiley:
But then after some time I saw question again and got that it has only two colors…

1 Like
8

@l_returns yes, I knew there were only two colours, but you can see in my competition code the fossils of the extended-problem thinking above.

9

  1. find count (g) of consecutive Green ones, increment g by 1 if first and last are green

  2. find count ® of consecutive Red ones, increment r by 1 if first and last are red

  3. if (r == 1 and g == 1) or (r == 0 and g == 0): print('yes') else: print('no')

  4. you have to make just 2 cuts, one for RR and another for GG, so there should be exactly 1 GG & 1 RR or none.

1 Like
10

You forgot to mention, that number of R and G should be equal. Rest fine :slight_smile:

11

Analyzing a bit more we can conclude that since we are only allowed to make one pair of cut, so the no. of consecutive flower pairs must be exactly 2 and that too the pairs must be of different colors(this justifies why the number of red and green flowers must be equal), else even after exchanging there will be at least one pair which would still be of same color.

12

@taran_1407 “R and G equal” follows automatically from the above assessment.

1 Like
13

Fortunately the case for only one flower is excluded from the problem, since an argument could be made for it being either beautiful or not beautiful. It depends on the criteria behind the “no pair of adjacent flowers with identical colours” definition. A simple reading allows it to be beautiful, but if the criterion is derived from needing variety, or considering a traverse along the garland and wanting a switch each time, a lone flower will not be beautiful.

I am well into over-thinking territory here.

1 Like
14

https://www.codechef.com/viewsolution/21673749

i have applied the concept that if length of garland is 1 then garland is beautiful else i hae counted number of R and G and if they are equal and their sum is even and then i have counted the mismatched pair and printed the result accordingly.

Can anyone please help me to figure out whats wrong…??