Can someone please explain the approach for this problem. The approach in the editorial is not clear.
Thanks!! 
4 Likes
That Q is definitely not “Very Very Easy” lol.
3 Likes
It’s very easy DP. But it need a little bit perfection on this. Give me some time, i will upload the full editorial of this question
Thanks! Your response is much awaited!!
Sorry for that. I still could not able to figure out the right way to explain you. It’s all about DP. There is getting a problem of manipulating the recursion formula given in the editorial
ok. But any simple explanation would be appreciated!! Thanks!!
We have got 2 conditions -
- eliminate single ball and pay 1 pound.
- eliminate 2 neighboring balls of same colors for no cost.
So we wil try to form a recursive solution which we will later memoize.
- We will have two pointers(index for given array) in our recursive function solve().
- solve(int i,int j)
{
}
- solve(int i,int j)
2.we take a temp variable to store the ith color in array.
- temp=ar[i];
3.Take a variable ans= some large value because we want the minimum answer.
4.Now we need a loop to generate different index between i and j.
- for(int k=i;k<=j;k++)
{
}
5.Now let’s see different conditions in the loop.
a. we check if(temp==ar[k]).
b. if(k==i) i.e it is the first element (i.e ith element) so we call the function-
ans=min(ans,1+solve(k+1,j));
since we have used ith ball which is only single ball so we add 1 and call the function from
k+1 to j.
c. if(k==j) i.e the last element -
ans=min(ans,solve(i+1,k-1));
since temp(which is 1 element was equal to ar[k] which means the first ball color(ith) is equal to last
ball (jth) color ,so we don’t have to pay for it and we just called the function from i+1 to k-1.
d. if both above case are not true this means k is in between i and j so it is simple to see that
ans=min(ans,solve(i+1,k-1)+solve(k+1,j));
leaving the first (ith) ball and kth ball we call the function.
6.Now we are left with the base cases-
We have 2 base cases because in last there are 2 conditions -
a. 1 ball left i.e i==j.
so we return 1 as only single ball left.
if(i==j)
{
return 1;
}
b. otherwise
if(i>j)
{
return 0;
}
-The memoization is simple which you can do by declaring a 2D array.
First try it yourself and for reference you can see my code
1 Like
Ok. So please give me more time. I am just little bit busy in our HINDU Methodology Holy festival.
I appreciate your effort but try to explain in more simple and precise language, if u can.
My approach is slightly different from what is described in the editorial, but I hope it will be easy to understand.
If a is our array of n balls, let f(i, j) be the cost of eliminating all the balls in a[i..j]. Our required solution is then f(0, n-1) (assuming 0-based indexing).
How do we calculate the value of f(i, j)?
If a[i]=a[j], let us eliminate all balls between i and j, then we can remove ball i and j with no cost. Hence in this case, f(i, j)=f(i+1, j-1).
If a[i] \ne a[j], let us split our given range into two pieces to be solved recursively. We cannot immediately say where is the best index for splitting hence we have to try all indices between i and j. In this case, f(i, j) = min\{f(i, k) + f(k+1, j) : i \le k \lt j\}
What about our base cases?
If i=j+1, then our range is empty, and f(i,j)=0.
If i=j, then we have one ball in our range which requires cost 1 to remove. So here f(i,j)=1.
Our final definition of f is as follows
f(i,j) = \begin{cases}
0 & \text{if } i=j+1, \\
1 & \text{if } i=j, \\
f(i+1,j-1) & \text{if } a[i]=a[j], \\
min\{f(i, k) + f(k+1, j) : i \le k \lt j\} & \text{otherwise}.
\end{cases}
The dynamic programming solution will require \mathcal{O}(n^2) space and \mathcal{O}(n^3) time.
For this problem the top-down approach is easier to implement. Here is the link to my solution.
As a challenge you can also try to implement a bottom-up approach
Hope this helps!
7 Likes
Nice explanation. Can you please present your views in regards of table filling DP? I mean how the approach given in editorial working?
Thanks for the solution and it would be good if you can provide a table filling DP solution!
In the editorial f(i,j) is said to be for the range i to j inclusive, but the solution described is for f(i,j) with i inclusive and j exclusive. There is another mistake in the editorial where “f(i-1,k+1) + f(k+1, j)” should be “f(i+1,k) + f(k+1, j)”. With these corrections I hope the explanation makes sense.
1 Like
I can easily interpret the mistake by looking through the solution. But i wanna know about how table is filling there?
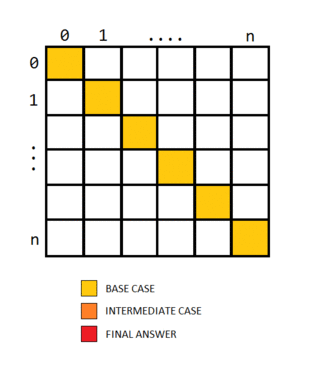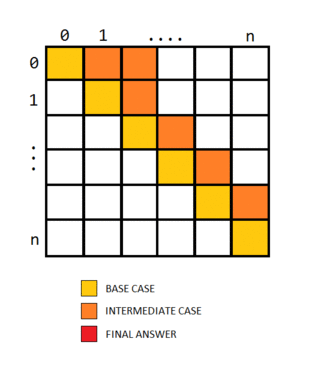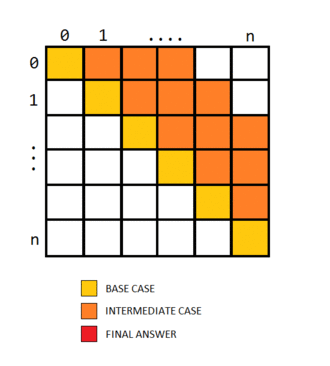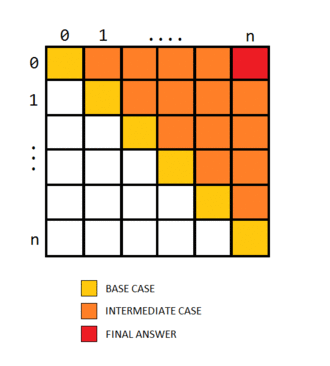
@bansal1232 by the editorial’s approach it is clear that the cases must be filled in increasing order of j-i, in other words the indices with i close to j must be filled first. Hence the solution fills in increasing order of the variable len. The base case for i=j is 0. The actual table filling would look something like this…
2 Likes
All right let me give a shot trying to explain you the solution.
Let me first define a state. I am taking (i,j) as a state which means the given array from index i to j inclusively.
Now, when I say answer for a state(i,j) that means the minimum moves required when i have an array from index i to j(inclusively).
n : size of array ( 0-based array )
Aim : we need to find the solution for the state (0,n-1) -> whole array.
How to accomplish it: we are going to collect answer for the desired state by taking the optimal combination of sub-states.
Okay, once again get back to state (0,n-1). Lets see the first element at index 0 i.e arr[0].
For first element we have two options either we will eliminate it individually (this will cost 1 move)
or
We will club it with some other index having same element as of arr[0].
lets say[ 0 , 1 , 2 , k1 , 4 , 5 , k2 , . . . , n-1 ] are the indices of the array.
and element at index 0 matches with element at index k1 and element at index k2
means arr[0] == arr[k1] == arr[k2].
Now once again get back to our answer for state concept.
Let's assume we have answer for all possible states (i,j) except state(0,n-1), which is the desired one.
So,we can say ans(0,n-1) = 1 + ans(1,n-1) // means we are eliminating arr[0] individually
Here, we have eliminated arr[0] individually so we add 1 to answer + we need to add answer for rest of array so we add the answer for the state (1,n-1).
or
0 1 2 k1 4 5 k2 .... n-1
------- ----------------------
ans(0,n-1) = ans(1,k1-1) + ans(k1+1,n-1)
This means we are clubbing idx 0 and k1 ( this counts 0 move ) ,but to do this we need to delete elements in between 0 and k1 , but as assumed we already the answer for that state(1,k1-1) + we also need to add the answer for array after k1 index because they are not eliminated so we will add answer for that state too i.e ans(k1+1,n-1)
or
0 1 2 k1 4 5 k2 .... n-1
------------------- ----------
ans(0,n-1) = ans(1,k2-1) + ans(k2+1,n-1)
Same above explaination.
So, ans(0,n-1) will be the minimum from above three conditions and hence, the question.
We will just put the above relation for states in recursion by initializing the base states.
Base States : ans(i,j) = 1 for all i == j
ans(i,j) = 0 for all i > j
My Solution : here .
1 Like
O…M…G!! Seriously meooow that’s AWESOME!!!
@meooow I implemented your solution but just kept
if dp[i][j] instead of dp[i][j] is not None
and my solution kept getting tle for tc 6. But writing is not None got ac in 2.9 sec which was earlier not getting ac in 25 sec. So do you know why ‘is not None’ so fast instead of the pythonic way?
Edit- Got it. Always thought they were same. Here