Problem Link
Author: Igor Barenblat
Tester: Misha Chorniy
Editorialist: Bhuvnesh Jain
Difficulty
MEDIUM-HARD
Prerequisites
Dynamic Convex-Hull Trick, Heavy-Light Decomposition
Problem
You are given a tree with N nodes. M speedsters travel on the tree. The i^{th} speedster starts at time t_i from vertex u_i and travels towards v_i at a constant speed of s_i. For every vertex, we need to find the first time, any speedster visited it. In case, it was not visited by any speedster, report the answer as -1.
Explanation
For simplicity, let us assume that the tree is rooted at node 1 and the depth of all vertices from the root is calculated. The depth is basically the distance of the vertex from the root of the tree i.e. 1.
Let us first write the equation for time taken by speedster i reach a vertex x. If the vertex doesn’t lie on the path from u_i to v_i then it is not visited by speedster i, or the time taken is INFINITY (a large constant). For all the other vertices on the directed path from u_i to v_i, the time taken is given by:
where lca(x, y) is the lowest common ancestor of vertices x and y.
We can now modify the equation for the time taken to reach any vertex on the path from u_i to v_i as follows:
Let the lowest common ancestor of u_i and v_i be lca. Calculate the final time at which we reach vertex v_i. Let us denote this by t_f. We now split the path from u_i to v_i into 2 parts: one from u_i to lca and from lca to v_i. NIte that these paths are directed. The image below shows how to calculate the time at any vertex x and y on the 2 different paths.
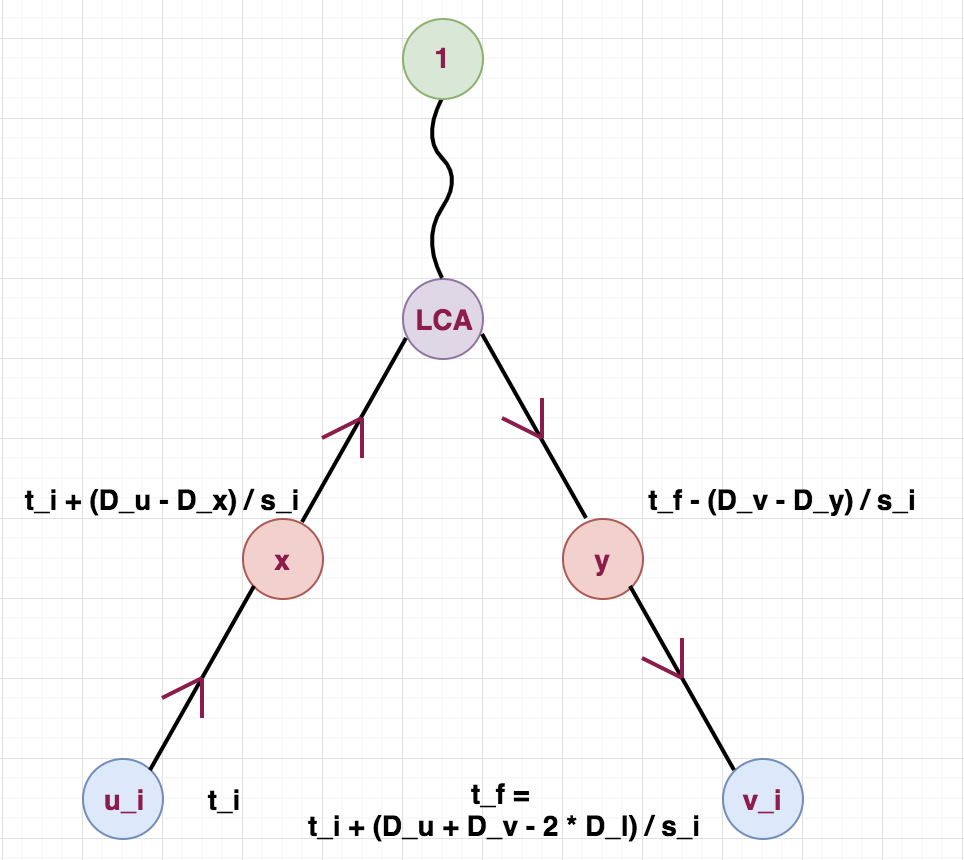
From the above figure, for a node x on path from u_i to lca, the time to reach it is:
Similarly, for a node y on path from lca to v_i, the time to reach it is:
If we observe carefully, both the above equations look the form Y = MX + C, where the first bracket part is C, time to be calculated is Y, \frac{1}{s_i} is the slope (M) and the depth of the node is X.
The problem asks us to find minimum time at which every node is visited by any speedster, and the above equations clearly show that time to reach it only depends on the depth of the node and pair (constant, slope) which is known beforehand for every speedster. Thus, this indicates the final solution will use the Dynamic convex-hull trick (Dynamic variant as the slopes are not guaranteed to be in increasing/decreasing order). If you don’t know about it or its use case, you can read it here
So, let us first try to solve a simple version of the problem where the tree is a bamboo(a straight path). This basically rules out the tree of the problem and reduces it to updates and queries of the following form on an array:
-
Update: Add a line (M, C) denoting Y = MX + C to every index in range [l, r].
-
Query: Find the minimum value at any index l for a given value of X = w.
We have range updates and point queries. So, we will use segment trees for the solution. In each node of the segment tree, we will keep the lines (represented by (M, C)) and for querying, we will just use the convex-hull trick to evaluate the minimum at node efficiently. Below is the pseudo-code for the segment-tree:
def init(t, i, j):
if i == j:
seg[t].clear() # remove all the lines
return
mid = (i+j)/2
init(2*t, i, mid)
init(2*t, mid+1, j)
def update(t, i, j, l, r, M, C):
if i > r or j < l:
return
if l <= i and j <= r:
# within required range
seg[t].add_line({M, C})
return
mid = (i+j)/2
update(2*t, i, mid, l, r, M, C)
update(2*t+1, mid+1, j, l, r, M, C)
def query(t, i, j, l, r, X):
if l <= i and j <= r:
return seg[t].evaluate_minimum(X)
mid = (i+j)/2
if i <= mid:
if j <= mid:
return query(2*t, i, mid, l, r, X)
else:
a = query(2*t, i, mid, l, r, X)
b = query(2*t+1, mid+1, j, l, r, X)
return min(a, b)
else:
return query(2*t+1, mid+1, j, l, r, X)
The time complexity of the above operations on segment tree is O(\log{N} * \log{M}) for both update and query. This is because each update and query will visit at most O(\log{N}) nodes and operation on every node (addition of a line or querying for minimum) is O(\log{M}). For a good reference code to the Dynamic convex hull, you can look up this.
Back to the tree problem. We see that we can easily handle queries on an array and the queries on the tree as basically those on a path. Voila, we can simply use Heavy light Decomposition or any other data structure you are suitable with (Euler Path or Centroid Decomposition). Thus, we efficiently solve the problem.
The overall time-complexity of the above approach using heavy-light decomposition will be O({\log}^{2}{N} * \log{M}) per update and query as it divides the path between the vertices u and v into O(\log{N}) path each of which is a straight path and can be solved using the segment tree mentioned above.
You can look at the author’s implementation for more details.
Feel free to share your approach, if it was somewhat different.
Time Complexity
O((N + M) * {\log}^{2}{N} * \log{M})
Space Complexity
O(N + M)
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.

