Problem link:
PREREQUISITES:
Bipartite matching , Konig’s theorem , binary search
PROBLEM:
In this problem , we were given N cats and N mice.We should choose K animals in such a way that maximum distance between any chosen cat and mice is minimum. Formally , suppose we chose n cats C1 , C2 … Cn and m mice - M1, M2 … Mm such that n+m = K , we want to choose them in such a way that max( dist(Ci,Mj) ) is minimized where 1 ≤ i ≤ n and 1 ≤ j ≤ m.Here dist gives the distance between ith chosen cat and jth chosen mice in 2D Cartesian coordinate plane.
EXPLANATION:
First we will discuss some definitions and then we will see how to solve this problem.
Maximum bipartite matching
A matching in a Bipartite Graph is a set of the edges chosen in such a way that no two edges share an endpoint. A maximum matching is a matching of maximum size (maximum number of edges). In a maximum matching, if any edge is added to it, it is no longer a matching. There can be more than one maximum matchings for a given Bipartite Graph.
vertex cover
A vertex cover of an undirected graph is a subset of its vertices such that for every edge (u, v) of the graph, either ‘u’ or ‘v’ is in vertex cover. Although the name is Vertex Cover, the set covers all edges of the given graph.The minimum vertex cover is the vertex cover having minimum size.
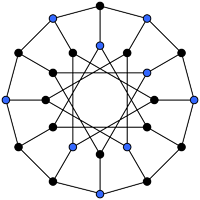
Independent Set
The independent set of the graph is set of vertices such that no two vertex in that set are adjacent to each other.The maximum independent set is the independent set having maximum size.The size of maximum independent set is total number of vertices minus minimum vertex cover.
In the above image , the nine blue vertices form a maximum independent set.
Konig’s Theorem
This theorem gives an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs.It says that in any bipartite graph, the number of edges in a maximum matching equals the number of vertices in a minimum vertex cover.

The bipartite graph shown in the above illustration has 14 vertices. A matching with six edges is shown in blue, and a vertex cover with six vertices is shown in red. There can be no smaller vertex cover, because any vertex cover has to include at least one endpoint of each matched edge (as well as of every other edge), so this is a minimum vertex cover. Similarly, there can be no larger matching, because any matched edge has to include at least one endpoint in the vertex cover, so this is a maximum matching. Konig’s theorem states that the equality between the sizes of the matching and the cover (in this example, both numbers are six) applies more generally to any bipartite graph.
Now lets see how to solve this problem.Suppose we fix the value of max( dist(Ci,Mj) ).Let D be the value of max( dist(Ci,Mj) ).The point to observe is if we can choose K animals whose max( dist(Ci,Mj) ) ≤ D , we can definitely choose K animals for values higher than D.However, if I decrease D , choosing K animals may or may not be possible.Thus we can see that existence of choosing of K animals is monotonic with increase in D.But why did we make this observation? This observation helps us to apply binary search on D.If we can find that we can choose K animals for any particular value of D , we will continue our search on lower values of D.So our problems reduces to find if we can choose K animals for any given value of D.If we can solve this problem , we will find minimum value of D using binary search such that its possible to choose K animals for that particular value of D.
Now lets see how to check if we can choose K animals using given D value.Lets build a graph containing only edges having weight ≥ D.That is , delete all the edges from the graph having weight < D.Now the point of observation is:
We can choose K animals only if the size of maximum independent set of this bipartite graph is atleast K.
But how to find the size of maximum independent set of this bipartite graph ? We can know the size of maximum independent set if we know the size of minimum vertex cover (since the size of maximum independent set is total number of vertices minus minimum vertex cover).But according to Konig’s theorem , the size of minimum vertex cover will be equal to number of edges in maximum bipartite matching.Thus we need to find the size of maximum bipartite matching in this graph.Lets assume its M.Thus we can choose K animals only if 2*N-M >= K.Follow this link if you want to know how to find maximum matching in a bipartite graph.